Cryptography: Theory and Practice:Zero-knowledge Proofs | Modern Cryptography: Theory and Practice

Cryptography: Theory and Practice
by Douglas Stinson
CRC Press, CRC Press LLC
ISBN: 0849385210 Pub Date: 03/17/95

Table of Contents

Exercises

13.1 Consider the interactive proof system for the problem Quadratic Non-residues presented in Figure 13.14. Prove that the system is sound and complete, and explain why the protocol is not zero-knowledge.

13.2 Devise an interactive proof system for the problem Subgroup Non-membership. Prove that your protocol is sound and complete.

13.3 Consider the zero-knowledge proof for Quadratic Residues that was presented in Figure 13.8.

(a) Define a valid triple to be one having the form (y, i, z), where y ∈ QR(n), i = 0 or 1,

and z² ≡ xⁱy (mod n). Show that the number of valid triples is 2(p - 1)(q - 1), and each such triple is generated with equal probability if Peggy and Vic follow the protocol.

(b) Show that Vic can generate triples having the same probability distribution without knowing the factorization n = pq.

(c) Prove that the protocol is perfect zero-knowledge for Vic.

13.4 Consider the zero-knowledge proof for Subgroup Membership that was presented in Figure 13.10.

(a) Prove that the protocol is sound and complete.

(b) Define a valid triple to be one having the form (γ, i, h), where

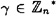, i = 0 or 1, 0 ≤ h ≤

- 1 and α^h ≡ βⁱγ (mod n). Show that the number of valid triples is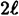

, and each such triple is generated with equal probability if Peggy and Vic follow the protocol.

(c) Show that Vic can generate triples having the same probability distribution without knowing the discrete logarithm log_α β.

(d) Prove that the protocol is perfect zero-knowledge for Vic.

13.5 Prove that the Discrete Logarithm bit commitment scheme presented in Section 13.5 is unconditionally concealing, and prove that it is binding if and only if Peggy cannot compute log_α β.

13.6 Suppose we use the Quadratic Residues bit commitment scheme presented in Section 13.5 to obtain a zero-knowledge argument for Graph 3-coloring. Using the forging algorithm presented in Figure 13.13, prove that this protocol is perfect zero-knowledge for Vic.

Table of Contents