MEAN OR EXPECTED VALUE

MEAN from RV Range: M discrete values or cells , X _k

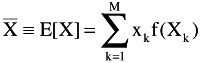
or MEAN from Sample Space: N discrete individual samples, S _i

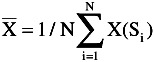
RANDOM EXPERIMENT

Sum produced by pair of fair six-sided dice.

Random Variable X _k defined as sum of the two numbers :

X _k = {D ₁ + D ₂ }

Cell k	No. in X k	X k	f (X k )	X k f (X k )
1	1	2	1/36	2/36
2	2	3	2/36	6/36
3	3	4	3/36	12/36
4	4	5	4/36	20/36
5	5	6	5/36	30/36
6	6	7	6/36	42/36
7	5	8	5/36	40/36
8	4	9	4/36	36/36
9	3	10	3/36	30/36
10	2	11	2/36	22/36
11	1	12	1/36	12/36
M = 11	36			Sum 252/36

Sample variance and standard deviation

1. Sample variance: Expected value of X _i about the mean

   

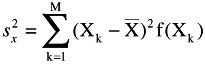
   or

   

2. Sample standard deviation: s _x ‰

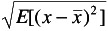
   Exercise: Sum of two fair dice: X _k = {D ₁ + D ₂ }

   x k	(X k - 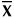)	(X k - 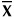) 2	f(X k )	(X k - 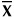) 2 f(X k )
   2	-5	25	1/36	25/36
   3	-4	16	2/36	32/36
   4	-3	9	3/36	27/36
   5	-2	4	4/36	16/36
   6	-1	1	5/36	5/36
   7			6/36
   8	1	1	5/36	5/36
   9	2	4	4/36	16/36
   10	3	9	3/36	27/36
   11	4	16	2/36	32/36
   12	5	25	1/36	25/36
   				Sum 210/36

   Variance:

   

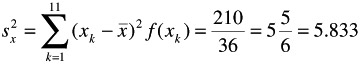
   Standard deviation:

   s _x = 2.415