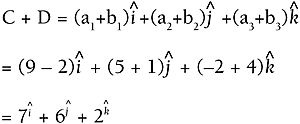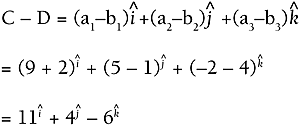Vector Addition and Subtraction

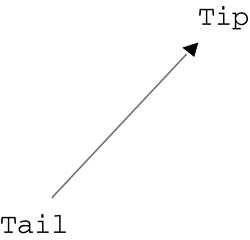
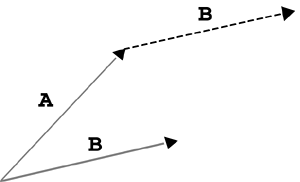
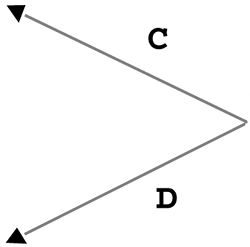
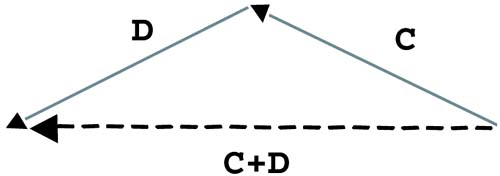
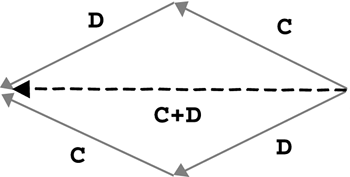
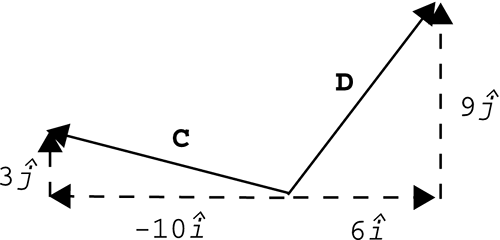
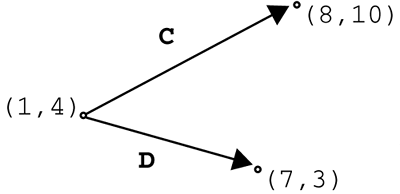
Whether your vectors represent displacements or velocities or forces, there might be times when you need to add or subtract them. We'll revisit this process in Chapters 10, 11, 12, and 14. We'll look at this process graphically first, and then we'll throw in the numbers .

When trying to organize vector quantities graphically, it is common to use an arrow for each vector. The arrow's length corresponds to the vector's magnitude, and the way it's pointing represents the direction. Because these arrows are drawn to scale, it's important to always work within the same scale (that is, all meters or all feet, but not both). That way, a vector with a magnitude of 5m appears to be half as long as a vector with a magnitude of 10m, as shown in Figure 4.6.

Figure 4.6. Two vectors represented by arrows.

We'll call the pointy end of the vector the tip and the other end the tail, as shown in Figure 4.7.

Figure 4.7. Vector tip and tail.

Now you can use the tip-to-tail method of adding vectors. One great thing about vectors is that they're not anchored to any one location. As long as the arrow stays the same length and keeps pointing in the same direction, it can be moved anywhere . To add two vectors graphically, just slide one so that it's tip-to-tail with the other, as shown in Figure 4.8.

Figure 4.8. Vector A tip-to-tail with vector B.

As soon as they're tip-to-tail, draw a new vector from the tail of the first one to the tip of the second one.

Think of the vectors shown in Figure 4.9 as displacement vectors on a road map. If you travel along vector A and then turn and follow vector B, you really go from the beginning of A to the end of B.

Figure 4.9. Vector A plus vector B.

Example 4.6: Adding Vectors Graphically

Find C + D for the vectors pictured in Figure 4.10.

Figure 4.10. Vectors C and D.

Solution

1. Slide vector D so that it's tip-to-tail with C. Be sure to keep D the same length and pointing in the same direction.

2. Draw a new vector C + D from the tail of C to the tip of D.

3. The final vector is shown in Figure 4.11.

   Figure 4.11. Vector C + D.

   

Look at the drawing of C + D. Notice that you could have also slid C tip-to-tail with D and gotten the same final vector (see Figure 4.12).

Figure 4.12. C + D = D + C.

Commutative Law of Vector Addition

A + B = B + A

for any vectors A and B.

Now try attaching some numbers to these vectors. You might have noticed in the preceding example that the length of vector C + D is much shorter than the length of C plus the length of D. That's because, with vectors, direction is taken into account. In other words:

For this reason, you cannot add vectors in polar coordinates unless they're in the same direction. Always convert vectors to Cartesian coordinates before attempting to add them. As soon as the two vectors are in Cartesian coordinates, just add "like" components . In other words, add the two and the two s.

Adding Vectors Numerically

for vectors and .

Example 4.7: Adding Vectors Numerically

Calculate C + D for vectors and .

Solution

1. Set this up graphically. Slide vector D so that it's tip-to-tail with C. Be sure to keep D the same length and pointing in the same direction.

2. Now draw a new vector C + D from the tail of C to the tip of D, as shown in Figure 4.13.

   Figure 4.13. Vector C + D again.

   

3. The only way to calculate C + D numerically is to calculate the total amount in the x direction and the total amount in the y direction. In other words, add the two components and add the two components. In this case:

   

   
   

   This is illustrated in Figure 4.14.

   Figure 4.14. Adding corresponding components.

   

NOTE

Notice that Example 4.7 starts with both vectors in Cartesian coordinates. If you had been planning in polar coordinates, you would first have to convert them and then add. You might need to refer to the preceding section for the conversion process.

The same method for adding vectors also applies to 3D. Again, the coordinates must be in Cartesian form for you to add them numerically.

Adding 3D Vectors Numerically

for vectors and .

Example 4.8: Adding 3D Vectors Numerically

Calculate C + D for 3D vectors and .

Solution

As you can see, adding vectors is quite simple when they're in Cartesian coordinates. Subtracting is equally simplejust subtract "like" components.

Subtracting Vectors Numerically

for vectors and .

The same process applies to 3D subtraction.

Subtracting 3D Vectors Numerically

for vectors and .

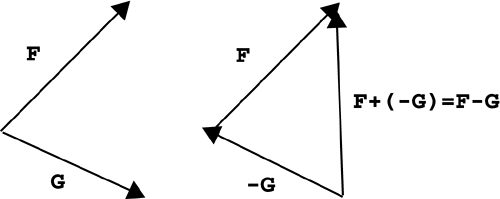
Notice that subtracting vectors is the same as adding the negative of the second vector. In other words, you flip the signs of each component in the second vector and then add. If you're trying to visualize this graphically, it's the same as flipping the direction of the second vector and then adding them tip-to-tail. This is illustrated in Figure 4.15.

Figure 4.15. Subtracting equals adding the negative.

Example 4.9: Subtracting 3D Vectors Numerically

Calculate C D for 3D vectors and .

Solution

So far, we have discussed two different forms of representing a vector: Cartesian coordinates (components) and polar coordinates (magnitude and direction). We've used the laws of right triangles (Pythagorean theorem and trigonometric functions) to convert between the two forms. Then we looked at adding and subtracting vectors in both 2D and 3D, which is fairly simple when the vectors are already in Cartesian coordinates. The next few sections look at how multiplication works with vectors.

Self-Assessment

1.	Convert vector A = 20ft @ 80 to Cartesian coordinates.
2.	Convert vector to polar coordinates.
3.	Using vectors A and B in the previous two questions, find the vector A + B.
4.	Using vectors A and B in the previous three questions, find the vector A B.
5.	Using vectors C and D shown in Figure 4.16, find vector C + D. Figure 4.16. Adding vectors C and D.
6.	Calculate F + G for 3D vectors and .
7.	Calculate F G for 3D vectors and .