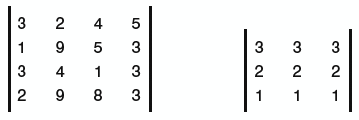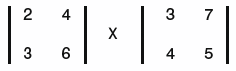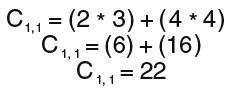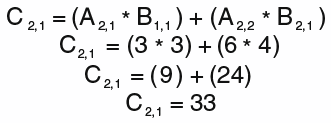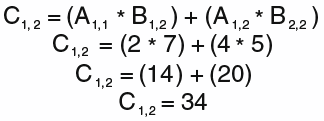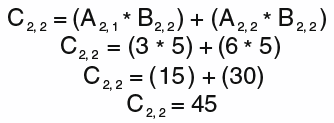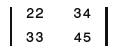Matrices

Ah, the matrix, by far the most esoteric and potentially "frightening" aspect of 3D programmers to the beginners who are just starting out. Things just appear so complicated when you jump in without a firm grasp of what's going on, but in reality, matrix math can be simple after you get used to it.

By definition, a matrix is a rectangular array where each entry contains a number, such as the following:

In this example, the first matrix is a 4x4 matrix and the second, a 3x3 matrix. (The numbers are completely arbitrary and have no bearing on the matrix itself.) Matrices are not required to be square; you could just as easily have a 4x1 matrix or a 1x18 matrix. The majority of work in 3D graphics and matrices uses a 4x4 matrix, and the Matrix class that is included in the Managed DirectX runtime is this type as well.

Why would you actually want to use matrices? Take this (extremely common) scenario. You have a model with say 50,000 vertices that you want to have rendered. However, before they are rendered, you want them rotated 90° on the x axis, rotated 180° around the y axis, scaled to twice the size they are now, and then moved 300 units to the left. As you can see, that is 2 rotations, 1 scale, and 1 translation, or a minimum of 12 math computations. For every single vertex in the model! You've come up with a whopping 600,000 math operations to transform your vertices the way you want.

What if you found out that with a single matrix, you could combine each of those four transformations and then use that one matrix to transform each of the coordinates? I'm sure you could understand why doing just over 50,000 math calculations is more desirable than doing 600,000. Even with the speed of modern processors, needlessly wasting time isn't anything you ever want to do.

Another benefit of using matrices is that every one of the transformation formulas you learned early can be expressed by a single matrix operation. This makes your code more readable as well as easier to understand because you don't have all these crazy algebra equations cluttering the code.

By far the most common operation you can perform on a matrix is multiplication. Although it's true that you can use built-in methods to perform this multiplication for you, it's important that you understand how the multiplication happens. For the basic 4x4 matrices that our 3D graphics programs use, what is the formula for the matrix multiplication? Don't be afraid of this function you're about to see:

What you're probably saying right now is "What in the heck is that?" Aside from looking bad, all it is really saying is that for each component in the new matrix C, you go through each row/column in the original matrices (A and B) and add them. Take two simple 2x2 matrices, such as these:

To multiply them together, you simply plug the values in the formula. For the first row/column of the new matrix, you use this formula:

The S (sigma) symbol is a fancy math character for a for loop, so the preceding formula breaks down like this:

Using the two entry matrices, plug in the actual values and you see the following:

Notice the order of the columns and vectors, particularly the A(1,2) and B(2,1). Did you expect the A(1,2) member to be 3 and the B(2,1) member to be 7? It is a common mistake that many people run into. Just to drive the point home, you should finish this matrix multiply:

What about C(1,2)?

Then, what about C(2,2)?

It gives you the resulting matrix C:

The same basic principle applies no matter how big your matrix is. Notice that the rules are slightly different if you're multiplying matrices of different sizes, but because that never happens in this book, I leave it as an exercise for you to figure out if you want. It's well beyond the scope of what this primer is intended for. To show that the basic principles are the same, here is the formula for calculating the first member of a 4x4 matrix multiplication:

Notice that it's the same formula you used for the 2x2 matrix; it's just that the sigma has been expanded to a larger for loop of four members rather than two.

Construction Cue

If you follow the algorithm through a few permutations (which I highly recommend), you'll notice that matrix multiplication is not commutative; that is, A*B does not equal B*A. For example, in the 2x2 matrix multiplication example, if the matrices were reversed, the resulting member of C(1,1) would have been 27, not 22. It's important to remember this point.

You might have noticed that you can think of the rows and columns of a matrix as somewhat like a vector. In fact, this is why you can use matrices to perform all your rotations. For example, when you have a matrix that has been translated (moved), you'll notice that the first three columns of row 4 will have the newly translated positions for the x, y, and z coordinates, respectively. Add in a new translation (through another matrix multiply), and you'll notice it's as if you did a vector add on those three components.

Consequently, scaling transformations are stored as C(1,1) x, C(2,2) y, and C(3,3) z in the matrix. Rotations are stored somewhat differently, depending on the axis of rotation, but the end result is that the first three members of column 0 end up facing the up direction (when normalized); the first three members of column 1 end up facing the right direction (when normalized); and the first three members of column 2 are the actual direction the object is facing (when normalized).

You'll notice many methods on the Matrix object that perform these operations for you. For example, to make a single matrix that rotates twice, scales, and translates (as described earlier,) you could write something like the following C# code:

 Matrix transformMatrix = Matrix.RotationY(1.0f) * Matrix.RotationZ(0.3f)  * Matrix.Scaling(15.0f) * Matrix.Translation(30.0f, 0.0f, 0.0f); 

Isn't that so much easier than reading the formulas that you learned just a few minutes ago?