10.2 Problems with Gaussian Elimination

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  10.   Solving Systems of Linear Equations

---

10.2 Problems with Gaussian Elimination

As we've seen, the Gaussian elimination algorithm, with its large number of arithmetic operations, is prone to roundoff errors. These errors become worse with larger systems of equations. Note that there are a number of subtractions and divisions, and as we saw back in Chapter 1, subtractions can lead to a loss of significant digits, and division by small values can magnify errors.

Some systems of equations are especially sensitive to roundoff errors. Slight changes in the coefficients of the intermediate systems during forward elimination can cause large changes in the final solution.

DEFINITION : A system of linear equations is ill-conditioned if small changes in the coefficients result in large changes in the solution.

DEFINITION : A system is well-conditioned if small changes in the coefficients result only in small changes in the solution.

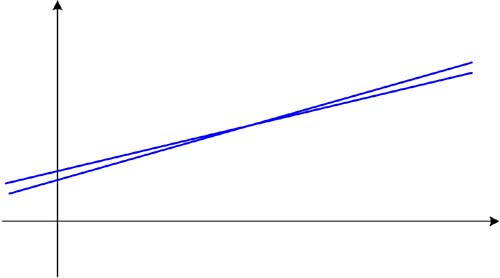
In Chapter 11, we'll compute a scalar value that measures a system's condition.

Figure 10-1 shows a simple example of an ill-conditioned system. Two lines are very nearly coincident. Even a tiny wiggle in either or both lines, caused by small changes in the coefficients of the two line equations, will cause a large change in the point where the lines cross.

Figure 10-1. A simple example of an ill-conditioned system. A tiny wiggle in either or both lines will greatly change where the two lines cross.

Another pitfall of Gaussian elimination is division by zero. If a pivot element is zero, then we're in trouble.

Gaussian elimination will fail if a system has no solution or if it has an infinite number of solutions. For example, in the simple case of two lines, the lines may be exactly coincident (an infinite number of solutions), or they may be parallel to each other (no solution).

DEFINITION : A system of linear equations is singular if it has no solution or an infinite number of solutions.

Thus, the straightforward form of the Gaussian elimination algorithm as shown in Section 10.1 is not enough. We need to make some improvements.

---

Top