| What if we don't have much prior knowledge of the numbers we're about to sum, such as how many there are and whether or not they're sorted? Perhaps the numbers are generated dynamically, and we need to know the current running sum at all times. Is there a way to add these numbers and avoid the magnitude problem? Figure 4-2 illustrates one solution to the magnitude problem, the Kahan Summation Algorithm, which is named after its developer. [1] This method is also called compensated summation. [1] William Kahan, a professor of computer science at the Berkeley campus of the University of California, does important work in the field of numerical computing. In the early 1980s, he led the group of computer scientists on the committee that wrote the IEEE 754 standard. He continues to consult with the computer industry to improve numerical computation. Figure 4-2. How the Kahan Summation Algorithm works. 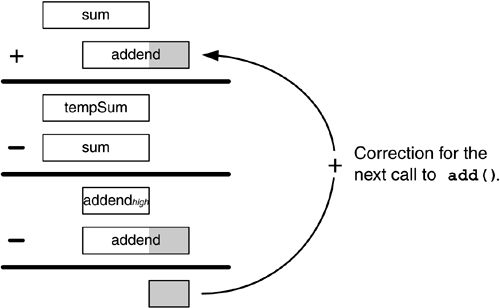 The algorithm uses feedback from the previous addition. During each addition, the new addend is "corrected" by adding to it an amount computed from the previous addition. The correction is the magnitude error, the rightmost bits of the previous addend that were lost when it was added to the running sum. By continuously recovering the lost bits from the previous addition, this summation algorithm manages to keep the running sum true despite the magnitude problems. Class Summation in package numbercruncher.mathutils implements this algorithm. See Listing 4-5a. Each call to method add() adds an addend and the correction to the running sum, and then it computes the correction for the next call. Listing 4-5a Kahan's Summation Algorithm for the float type. package numbercruncher.mathutils; /** * Implement Kahan's Summation Algorithm for the float type. */ public class KahanSummation { /** the current running sum */ private float sum; /** the current correction */ private float correction; /** the current corrected addend */ private float correctedAddend; /** * Constructor. */ public KahanSummation() {} /** * Return the current corrected value of the running sum. * @return the running sum's value */ public float value() { return sum + correction; } /** * Return the corrected value of the current addend. * @return the corrected addend value */ public float correctedAddend() { return correctedAddend; } /** * Add the value of an addend to the running sum. * @param the addend value */ public void add(float addend) { // Correct the addend value and add it to the running sum. correctedAddend = addend + correction; float tempSum = sum + correctedAddend; // Compute the next correction and set the running sum. // The parentheses are necessary to compute the high-order // bits of the addend. correction = correctedAddend - (tempSum - sum); sum = tempSum; } /** * Clear the running sum and the correction. */ public void clear() { sum = 0; correction = 0; } } Program 4 C5, shown in Listing 4-5b, uses class Summation to compute our fraction sum for denominator s 100,000,000 . As we can see from the output, there is a significant improvement in the accuracy of the final sum, despite the high percentages of exponent differences within each group that exceed 24. Listing 4-5b Fraction sums for n = 100,000,000 by the Kahan Summation Algorithm. package numbercruncher.program4_5; import numbercruncher.mathutils.KahanSummation; import numbercruncher.mathutils.AlignRight; /** * PROGRAM 4-5: Fraction Sum 100M by the Kahan Summation Algorithm * * Use the Kahan Summation Algorithm to compute * the sum 1/d + 2/d + 3/d + ... + n/d = d/d * where: * n = 100,000,000 * d = 1 + 2 + 3 + ... + n = (n/2)(n + 1) * * See if the sum is closer to 1. */ public class FractionSum100MKahan { private static final int GROUPS = 20; private static final int MAX = 100000000; // 100M public static void main(String args[]) { AlignRight ar = new AlignRight(); ar.print("i", 9); ar.print("Running sum", 16); ar.print("% ExpDiff>24", 16); ar.underline(); float denom = (0.5f*MAX)*(MAX + 1); KahanSummation kSum = new KahanSummation(); int gSize = MAX/GROUPS; // group size int gEnd = gSize; // index of group end int exceeds = 0; // # of exponent diff > 24 // Sum the corrected fractions. for (int i = 1; i <= MAX; ++i) { float fraction = i/denom; int expSum = Float.floatToIntBits(kSum.value()) >> 23; kSum.add(fraction); int expFraction = Float.floatToIntBits( kSum.correctedAddend()) >> 23; int diff = Math.abs(expSum - expFraction); if ((i > 1) && (diff > 24)) ++exceeds; // Printout at the start of each group. if (i == gEnd) { ar.print(i, 9); ar.print(kSum.value(), 16); ar.print((100*exceeds)/gSize, 16); ar.println(); exceeds = 0; gEnd += gSize; } } System.out.println("\n% error = " + 100*Math.abs(kSum.value() - 1)); } } Output: i Running sum % ExpDiff>24 ----------------------------------------- 5000000 0.0025000004 0 10000000 0.010000001 0 15000000 0.0225 0 20000000 0.04 0 25000000 0.0625 0 30000000 0.09 26 35000000 0.1225 12 40000000 0.16 46 45000000 0.2025 42 50000000 0.25 36 55000000 0.3025 64 60000000 0.35999998 61 65000000 0.42249998 58 70000000 0.48999998 54 75000000 0.5625 72 80000000 0.64 73 85000000 0.72249997 72 90000000 0.81 70 95000000 0.9025 68 100000000 1.0 67 % error = 0.0 Figure 4-3 shows this improvement dramatically the running sum of Program 4 C5 smoothly increases to 1. Figure 4-3. The smoothly increasing running sum of Program 4 C5, thanks to the Kahan Summation Algorithm.  | 

