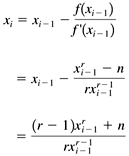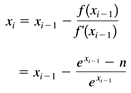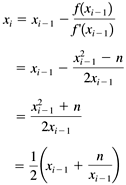12.5 Big Decimal Functions
12.5 Big Decimal Functions The BigDecimal class does not include methods such as sqrt() , exp() , or ln() , and so we need to write them ourselves . Listing 12-2a shows class BigFunctions in package numbercruncher.mathutils , where we implement several useful functions. (These functions are useful because we need them in the next chapter!) We use some of the algorithms from Chapters 2, 4, and 5. Listing 12-2a Class BigFunctions , which implements several useful BigDecimal functions. package numbercruncher.mathutils; import java.math.BigInteger; import java.math.BigDecimal; /** * Several useful BigDecimal mathematical functions. */ public final class BigFunctions { /** * Compute x^exponent to a given scale. Uses the same * algorithm as class numbercruncher.mathutils.IntPower. * @param x the value x * @param exponent the exponent value * @param scale the desired scale of the result * @return the result value */ public static BigDecimal intPower(BigDecimal x, long exponent, int scale) { // If the exponent is negative, compute 1/(x^-exponent). if (exponent < 0) { return BigDecimal.valueOf(1) .divide(intPower(x, -exponent, scale), scale, BigDecimal.ROUND_HALF_EVEN); } BigDecimal power = BigDecimal.valueOf(1); // Loop to compute value^exponent. while (exponent > 0) { // Is the rightmost bit a 1? if ((exponent & 1) == 1) { power = power.multiply(x) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); } // Square x and shift exponent 1 bit to the right. x = x.multiply(x) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); exponent >>= 1; Thread.yield(); } return power; } /** * Compute the integral root of x to a given scale, x >= 0. * Use Newton's algorithm. * @param x the value of x * @param index the integral root value * @param scale the desired scale of the result * @return the result value */ public static BigDecimal intRoot(BigDecimal x, long index, int scale) { // Check that x >= 0. if (x.signum() < 0) { throw new IllegalArgumentException("x < 0"); } int sp1 = scale + 1; BigDecimal n = x; BigDecimal i = BigDecimal.valueOf(index); BigDecimal im1 = BigDecimal.valueOf(index-1); BigDecimal tolerance = BigDecimal.valueOf(5) .movePointLeft(sp1); BigDecimal xPrev; // The initial approximation is x/index. x = x.divide(i, scale, BigDecimal.ROUND_HALF_EVEN); // Loop until the approximations converge // (two successive approximations are equal after rounding). do { // x^(index-1) BigDecimal xToIm1 = intPower(x, index-1, sp1); // x^index BigDecimal xToI = x.multiply(xToIm1) .setScale(sp1, BigDecimal.ROUND_HALF_EVEN); // n + (index-1)*(x^index) BigDecimal numerator = n.add(im1.multiply(xToI)) .setScale(sp1, BigDecimal.ROUND_HALF_EVEN); // (index*(x^(index-1)) BigDecimal denominator = i.multiply(xToIm1) .setScale(sp1, BigDecimal.ROUND_HALF_EVEN); // x = (n + (index-1)*(x^index)) / (index*(x^(index-1))) xPrev = x; x = numerator .divide(denominator, sp1, BigDecimal.ROUND_DOWN); Thread.yield(); } while (x.subtract(xPrev).abs().compareTo(tolerance) > 0); return x; } /** * Compute e^x to a given scale. * Break x into its whole and fraction parts and * compute (e^(1 + fraction/whole))^whole using Taylor's formula. * @param x the value of x * @param scale the desired scale of the result * @return the result value */ public static BigDecimal exp(BigDecimal x, int scale) { // e^0 = 1 if (x.signum() == 0) { return BigDecimal.valueOf(1); } // If x is negative, return 1/(e^-x). else if (x.signum() == -1) { return BigDecimal.valueOf(1) .divide(exp(x.negate(), scale), scale, BigDecimal.ROUND_HALF_EVEN); } // Compute the whole part of x. BigDecimal xWhole = x.setScale(0, BigDecimal.ROUND_DOWN); // If there isn't a whole part, compute and return e^x. if (xWhole.signum() == 0) return expTaylor(x, scale); // Compute the fraction part of x. BigDecimal xFraction = x.subtract(xWhole); // z = 1 + fraction/whole BigDecimal z = BigDecimal.valueOf(1) .add(xFraction.divide( xWhole, scale, BigDecimal.ROUND_HALF_EVEN)); // t = e^z BigDecimal t = expTaylor(z, scale); BigDecimal maxLong = BigDecimal.valueOf(Long.MAX_VALUE); BigDecimal result = BigDecimal.valueOf(1); // Compute and return t^whole using intPower(). // If whole > Long.MAX_VALUE, then first compute products // of e^Long.MAX_VALUE. while (xWhole.compareTo(maxLong) >= 0) { result = result.multiply( intPower(t, Long.MAX_VALUE, scale)) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); xWhole = xWhole.subtract(maxLong); Thread.yield(); } return result.multiply(intPower(t, xWhole.longValue(), scale)) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); } /** * Compute e^x to a given scale by the Taylor series. * @param x the value of x * @param scale the desired scale of the result * @return the result value */ private static BigDecimal expTaylor(BigDecimal x, int scale) { BigDecimal factorial = BigDecimal.valueOf(1); BigDecimal xPower = x; BigDecimal sumPrev; // 1 + x BigDecimal sum = x.add(BigDecimal.valueOf(1)); // Loop until the sums converge // (two successive sums are equal after rounding). int i = 2; do { // x^i xPower = xPower.multiply(x) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); // i! factorial = factorial.multiply(BigDecimal.valueOf(i)); // x^i/i! BigDecimal term = xPower .divide(factorial, scale, BigDecimal.ROUND_HALF_EVEN); // sum = sum + x^i/i! sumPrev = sum; sum = sum.add(term); ++i; Thread.yield(); } while (sum.compareTo(sumPrev) != 0); return sum; } /** * Compute the natural logarithm of x to a given scale, x > 0. */ public static BigDecimal ln(BigDecimal x, int scale) { // Check that x > 0. if (x.signum() <= 0) { throw new IllegalArgumentException("x <= 0"); } // The number of digits to the left of the decimal point. int magnitude = x.toString().length() - x.scale() - 1; if (magnitude < 3) { return lnNewton(x, scale); } // Compute magnitude*ln(x^(1/magnitude)). else { // x^(1/magnitude) BigDecimal root = intRoot(x, magnitude, scale); // ln(x^(1/magnitude)) BigDecimal lnRoot = lnNewton(root, scale); // magnitude*ln(x^(1/magnitude)) return BigDecimal.valueOf(magnitude).multiply(lnRoot) .setScale(scale, BigDecimal.ROUND_HALF_EVEN); } } /** * Compute the natural logarithm of x to a given scale, x > 0. * Use Newton's algorithm. */ private static BigDecimal lnNewton(BigDecimal x, int scale) { int sp1 = scale + 1; BigDecimal n = x; BigDecimal term; // Convergence tolerance = 5*(10^-(scale+1)) BigDecimal tolerance = BigDecimal.valueOf(5) .movePointLeft(sp1); // Loop until the approximations converge // (two successive approximations are within the tolerance). do { // e^x BigDecimal eToX = exp(x, sp1); // (e^x - n)/e^x term = eToX.subtract(n) .divide(eToX, sp1, BigDecimal.ROUND_DOWN); // x - (e^x - n)/e^x x = x.subtract(term); Thread.yield(); } while (term.compareTo(tolerance) > 0); return x.setScale(scale, BigDecimal.ROUND_HALF_EVEN); } /** * Compute the arctangent of x to a given scale, x < 1 * @param x the value of x * @param scale the desired scale of the result * @return the result value */ public static BigDecimal arctan(BigDecimal x, int scale) { // Check that x < 1. if (x.abs().compareTo(BigDecimal.valueOf(1)) >= 0) { throw new IllegalArgumentException("x >= 1"); } // If x is negative, return -arctan(-x). if (x.signum() == -1) { return arctan(x.negate(), scale).negate(); } else { return arctanTaylor(x, scale); } } /** * Compute the arctangent of x to a given scale * by the Taylor series, x < 1 * @param x the value of x * @param scale the desired scale of the result * @return the result value */ private static BigDecimal arctanTaylor(BigDecimal x, int scale) { int sp1 = scale + 1; int i = 3; boolean addFlag = false; BigDecimal power = x; BigDecimal sum = x; BigDecimal term; // Convergence tolerance = 5*(10^-(scale+1)) BigDecimal tolerance = BigDecimal.valueOf(5) .movePointLeft(sp1); // Loop until the approximations converge // (two successive approximations are within the tolerance). do { // x^i power = power.multiply(x).multiply(x) .setScale(sp1, BigDecimal.ROUND_HALF_EVEN); // (x^i)/i term = power.divide(BigDecimal.valueOf(i), sp1, BigDecimal.ROUND_HALF_EVEN); // sum = sum +- (x^i)/i sum = addFlag ? sum.add(term) : sum.subtract(term); i += 2; addFlag = !addFlag; Thread.yield(); } while (term.compareTo(tolerance) > 0); return sum; } /** * Compute the square root of x to a given scale, x >= 0. * Use Newton's algorithm. * @param x the value of x * @param scale the desired scale of the result * @return the result value */ public static BigDecimal sqrt(BigDecimal x, int scale) { // Check that x >= 0. if (x.signum() < 0) { throw new IllegalArgumentException("x < 0"); } // n = x*(10^(2*scale)) BigInteger n = x.movePointRight(scale << 1).toBigInteger(); // The first approximation is the upper half of n. int bits = (n.bitLength() + 1) >> 1; BigInteger ix = n.shiftRight(bits); BigInteger ixPrev; // Loop until the approximations converge // (two successive approximations are equal after rounding). do { ixPrev = ix; // x = (x + n/x)/2 ix = ix.add(n.divide(ix)).shiftRight(1); Thread.yield(); } while (ix.compareTo(ixPrev) != 0); return new BigDecimal(ix, scale); } } As we did in our class numbercruncher.mathutils.IntPower (see Chapter 2), method intPower() partitions the exponent into the sum of powers of 2. Note that, after each multiplication, it resets the scale. Otherwise, the scales of the intermediate results will grow with each iteration. There is also a call to Thread.yield() in each iteration. Method intRoot() computes any integral root r of a number using Newton's algorithm: where n is the number whose r th root we wish to compute, and To speed convergence, method exp() computes e x by breaking the exponent into its whole and fractional components and then computing (See Chapter 4.) The method uses the Taylor series for e x , as implemented by the private method expTaylor() . If the value of whole is greater than Long.MAX_VALUE , then it partitions whole into the sum of addends of Long.MAX_VALUE and multiplies together the values of each e Long.MAX_VALUE . Method ln() computes a natural logarithm. The Taylor series is for x > 0, but since the where n is the value whose natural logarithm we want to find and This is implemented by the private method lnNewton() . So now how fast we can compute ln x depends on how fast we can compute e x . If the value of x is large, method exp() will execute slowly. Therefore, method ln() employs a simple "strength reduction"?alet m be the magnitude (the number of digits to the left of the decimal point) of x. Then, if m > 3, instead of computing ln x, the method computes instead This is faster because method intPower() uses Newton's algorithm, which converges more rapidly than the Taylor series used by method expTaylor() . Method arctan() uses the Taylor series for x < 1. Because computing a square root is a common operation, class BigFunctions has a special optimized method sqrt() . The method first "scales up" to BigInteger whole numbers with the equivalent of multiplying by even powers of 10, and then it uses the faster integer arithmetic. It applies Newton's algorithm, and then it "scales down" the result to the appropriate BigDecimal value. The implementation of Newton's algorithm is similar to what we saw in Chapter 5: where n is the number whose square root we wish to compute, and each approximation x i is The method goes one step further to avoid the Listing 12-2b shows Program 12 §C2, which tests the methods in class BigFunctions by comparing results with those obtained with methods from class java.lang.Math . Listing 12-2b Testing class BigFunctions . package numbercruncher.program12_2; import java.math.BigDecimal; import numbercruncher.mathutils.BigFunctions; /** * PROGRAM 12-2: Test BigFunctions * * Test the BigFunctions by comparing results with * class java.lang.Math. */ public class TestBigFunctions { private static final int SCALE = 40; /** * Run the test. */ private void run() { System.out.println("2^(-25) = " + Math.pow(2, -25)); System.out.println(" = " + BigFunctions.intPower(BigDecimal.valueOf(2), -25, SCALE)); System.out.println(); System.out.println("sqrt 2 = " + Math.sqrt(2)); System.out.println(" = " + BigFunctions.sqrt(BigDecimal.valueOf(2), SCALE)); System.out.println(); System.out.println("2^(1/3) = " + Math.exp(Math.log(2)/3)); System.out.println(" = " + BigFunctions.intRoot(BigDecimal.valueOf(2), 3, SCALE)); System.out.println(); System.out.println("e^(-19.5) = " + Math.exp(-19.5)); System.out.println(" = " + BigFunctions.exp(new BigDecimal("-19.5"), SCALE)); System.out.println(); System.out.println("ln 2 = " + Math.log(2)); System.out.println(" = " + BigFunctions.ln(BigDecimal.valueOf(2), SCALE)); System.out.println(); System.out.println("arctan sqrt(3)/3 = " + Math.PI/6); System.out.println(" = " + BigFunctions.arctan( BigFunctions.sqrt(BigDecimal.valueOf(3), SCALE) .divide(BigDecimal.valueOf(3), SCALE, BigDecimal.ROUND_HALF_EVEN), SCALE)); } /** * Main. * @param args the array of program arguments */ public static void main(String args[]) { TestBigFunctions test = new TestBigFunctions(); try { test.run(); } catch(Exception ex) { System.out.println("ERROR: " + ex.getMessage()); } } } Output: 2^(-25) = 2.9802322387695312E-8 = 0.0000000298023223876953125000000000000000 sqrt 2 = 1.4142135623730951 = 1.4142135623730950488016887242096980785696 2^(1/3) = 1.2599210498948732 = 1.25992104989487316476721060727822835057024 e^(-19.5) = 3.398267819495071E-9 = 0.0000000033982678194950712251407378768109 ln 2 = 0.6931471805599453 = 0.6931471805599453094172321214581765680755 arctan sqrt(3)/3 = 0.5235987755982988 = 0.52359877559829887307710723054658381403285 Of course, we can write many more BigFunctions methods, but these are the ones we'll need for Chapter 13. They can serve as models for any more methods we may choose to write later.  |
terms are close to 1 for large values of 
term, which would double the number of digits of precision. (There is no setScale() method for BigInteger values.) Multiplying by 
is a simple shift to the right by 1 bit. | |
| Top |
EAN: 2147483647
Pages: 141