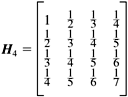11.5 Hilbert Matrices

---

 

	Java Number Cruncher: The Java Programmer's Guide to Numerical Computing By Ronald  Mak
	Table of Contents
	Chapter  11.   Matrix Inversion, Determinants, and Condition Numbers

---

11.5 Hilbert Matrices

Program 11-1 exercises our ability to compute the inverse of a matrix with a Hilbert matrix. A Hilbert matrix H _n is a square n x n matrix whose elements are defined as

For example,

It turns out that Hilbert matrices are extremely ill-conditioned with very high condition numbers; therefore, they are notoriously difficult to invert accurately. Program 11-1 demonstrates this with the 4 x 4 Hilbert matrix. See Listing 11-1.

Listing 11-1 Demonstrate the matrix inversion algorithm with a Hilbert matrix.

 package numbercruncher.program11_1; import numbercruncher.matrix.*; /**  * PROGRAM 11-1: Hilbert Matrices  *  * Test the matrix inverter with a Hilbert matrix.  Hilbert matrices are  * ill-conditioned and difficult to invert accurately.  */ public class HilbertMatrix {     private static final int RANK = 4;     private void run(int rank) throws MatrixException     {         System.out.println("Hilbert matrix of rank " + rank);         InvertibleMatrix H = new InvertibleMatrix(rank);         // Compute the Hilbert matrix.         for (int r = 0; r < rank; ++r) {             for (int c = 0; c < rank; ++c) {                 H.set(r, c, 1.0f/(r + c + 1));             }         }         H.print(15);         // Invert the Hilbert matrix.         InvertibleMatrix Hinv = H.inverse();         System.out.println("\nHilbert matrix inverted");         Hinv.print(15);         System.out.println(""\nHilbert matrix condition number = " +                            H.norm()*Hinv.norm());         // Invert the inverse.         InvertibleMatrix HinvInv = Hinv.inverse();         System.out.println("\nInverse matrix inverted");         HinvInv.print(15);         // Multiply P = H*Hinv.         System.out.println("\nHilbert matrix times its inverse " +                            "(should be identity)");         SquareMatrix P = H.multiply(Hinv);         P.print(15);         // Average norm of P's rows.         float normSum = 0;         for (int r = 0; r < rank; ++r) {             normSum += P.getRow(r).norm();         }         System.out.println("\nAverage row norm = " + normSum/rank +                            " (should be 1)");     }     /**      * Main.      * @param args the array of arguments      */     public static void main(String args[])     {         HilbertMatrix test = new HilbertMatrix();         try {             test.run(RANK);         }         catch(MatrixException ex) {             System.out.println("*** ERROR: " + ex.getMessage());             ex.printStackTrace();         }     } } 

Output:

 Hilbert matrix of rank 4 Row  1:            1.0            0.5     0.33333334           0.25 Row  2:            0.5     0.33333334           0.25            0.2 Row  3:     0.33333334           0.25            0.2     0.16666667 Row  4:           0.25            0.2     0.16666667     0.14285715 Hilbert matrix inverted Row  1:      15.999718      -119.9972      239.99367     -139.99605 Row  2:      -119.9972      1199.9725     -2699.9382      1679.9615 Row  3:      239.99367     -2699.9382       6479.862      -4199.914 Row  4:     -139.99605      1679.9615      -4199.914      2799.9465 Hilbert matrix condition number = 15613.463 Inverse matrix inverted Row  1:      0.9999907     0.49999347     0.33332846     0.24999614 Row  2:     0.49999347     0.33332878      0.2499966     0.19999732 Row  3:     0.33332846      0.2499966     0.19999747     0.16666469 Row  4:     0.24999614     0.19999732     0.16666469     0.14285558 Hilbert matrix times its inverse (should be identity) Row  1:            1.0   3.0517578E-5   1.2207031E-4  -6.1035156E-5 Row  2:  -3.8146973E-6            1.0            0.0  -6.1035156E-5 Row  3:  -3.8146973E-6            0.0            1.0  -3.0517578E-5 Row  4:            0.0   1.5258789E-5   6.1035156E-5     0.99993896 Average row norm = 0.99998474 (should be 1) 

As we can see from the output, although all the elements of H ₄ are less than or equal to 1, the elements of its inverse can be several orders of magnitude larger. The condition number of H ₄ is nearly 16,000, indicating that it is very ill-conditioned.

Because of their high condition numbers, we cannot reliably invert Hilbert matrices larger than 6 x 6 using single-precision arithmetic and LU decomposition.

---

Top