Chapter 9: Linked Data Structures

Overview

Fundamentals, advantages, and disadvantages of linked data structures. Moving a linked data structure in memory, or to/from a disk, or transmitting it across a communication channel - techniques of compaction and serialization. Memory allocation from a specific arena.

Linked data structures are intimately related to memory, where they are created, located, and processed . Naturally for this book, this relationship with memory is our principal focus in this chapter. It is not our intention to provide a comprehensive presentation of linked data structures in C or C++ and their applications. There are many excellent books on the topic of algorithms and data structures, particularly in C and C++.

Linked data structures and their applications are one of the great successes of the early decades of computer science. The reader can easily imagine how useful software would be if it worked solely with numbers and arrays. But how then would we model and program such things as lists, graphs, stacks, queues, charts , diagrams, and many other abstract notions that are needed to deal with today's complex programming tasks ?

Philosophically, a linked approach to data structures is used for any of the following reasons: the data structure must be created dynamically; each part of it is created at a different time; the mutual relations of the parts change in time. Sometimes links are used as a "physical" implementation of "logical relations" (the best example would be databases and the use of foreign keys as "links"). Technically, linked data structures are built in a simple sequence: (i) create a part and (ii) link it with the structure. This simple sequence is repeated many times, often in a recursive manner. A typical example would be a linked list, but it is a bit too simple for some of the aspects we wish to discuss. Hence we have decided to use trees - as ubiquitous and well- understood as lists, and nicely treatable in recursive ways.

We will illustrate the issues using simple binary search trees for characters . Such a tree is a binary tree (each node has at most two children), each node stores a character value, and the value stored in the left (resp., right) child is smaller (resp., larger) than the value stored in the parent node. Among the nice properties of such a tree are: a search for a value has the average-case complexity O (log n ), where n is the number of elements stored in the tree; and in-order traversal of the tree lists the characters stored in the tree in an ascending order.

Let us consider a classical recursive function Insert() , which inserts (creates and links) a new node for a given character c , and a recursive function Show() performing in-order traversal of the tree:

 struct NODE_STRUCT {   char value;   struct NODE_STRUCT* lch;   /* link to left child */   struct NODE_STRUCT* rch;   /* link to right child */ }; typedef struct NODE_STRUCT NODE; typedef struct NODE_STRUCT* PNODE; /* function Insert -------------------------------------------- */ NODE Insert(PNODE n,char c) {   if (n == NULL) { /* at the end of path, or tree not built yet */     if ((n = malloc(sizeof(NODE))) == NULL) merror();     n->value = c;     n->lch = n->rch = NULL;     return n;   }   if (c < n->value)  /* go left */     n->lch = Insert(n->lch,c);   else               /* go right */     n->rch = Insert(n->rch,c);   return n; }/*end Insert*/ /* function Show ---------------------------------------------- */ void Show(PNODE n) {   if (n == NULL) return;   Show(n->lch);   printf(" %c",n->value);   Show(n->rch); }/*end Show*/ 

For the sake of simplicity, we made Insert() return the "root" every time so we do not have to pass the root by reference (which in C can only be emulated). Thus, every time a character c is to be inserted in the tree with root tree , one must use tree = Insert(tree,c) . (To keep the sample code as simple as possible, we also skipped dealing with insertion of a value already stored in the tree.) Show(tree) will display the list of characters stored in the tree in ascending order.

The first topic we would like to discuss is the nature of links. In the previous example we used pointers, which are quite suitable to the task. However, we may use something else. In our next example we have Insert1() and Show1() do likewise - build a search tree and traverse it, displaying the nodes visited in order - while using arrays and array indexes instead of pointers.

 #define null -1    typedef int PNODE1;   /* a node */    char value[100];      /* value */    int lch[100];         /* left child links */    int rch[100];         /* right child links */    int mem = null;       /* fake top of memory */    /* function Insert1 -------------------------------------- */    PNODE1 Insert1(PNODE1 n,char c)    {      if (n == null) {        n = ++mem;        value[n] = c;        lch[n] = rch[n] = null;        return n;      }      if (c < value[n])        lch[n] = Insert1(lch[n],c);      else        rch[n] = Insert1(rch[n],c);      return n;    }/*end Insert1*/    /* function Show1 ---------------------------------------- */    void Show1(PNODE1 n)    {      if (n == null) return;      Show1(lch[n]);      printf(" %c",value[n]);      Show1(rch[n]);    }/*end Show1*/ 

For a tree with up to100 nodes, this will work as well as Insert() . In Chapter 6 we mentioned that arrays are such faithful models of memory that they can actually be used as memory, which is exactly what we have done here. However, using the arrays is rather a "static" approach - if the tree has only a few nodes then most of the memory is wasted , and if the tree needs more than 100 then it cannot be accommodated - unless the arrays themselves are dynamic (see Chapter 6). Nevertheless, we might consider this approach if we needed a simple and natural way to serialize the tree. We will discuss that topic later in the chapter.

The function Insert() (in the first example of this chapter) builds the tree completely on the heap. However, it is possible to build a linked data structure on the stack, as our next example demonstrates . Building on the stack is not usually advisable, but for some special cases it may be considered . In the code of the next example, List() is basically a recursive descent parser for a list of characters separated by commas. The function Next() (its scanner) returns the character it scanned, or -2 if it scanned a comma, or -1 when the end of the input string s is reached. Here sp - the string position indicator - is passed by reference for the sake of simpler code; only for that reason are we using C++ rather than C. List() builds the tree from multiple versions of the node n , which is a local auto variable, and so the tree is completely built on the system stack. The tree is used only at the bottom of the descent, when the whole input has been parsed. This is the point at which the whole tree is available and can be traversed by Show() as before. For this reason, the insertion of each new node is done via iteration rather than recursion (as in the previous examples). The advantage of such a linked data structure can be summarized simply: no explicit memory allocation is needed and hence there is no need for memory deallocation - unwinding of the stack will take care of the deallocation. The disadvantage is that such a data structure is only available to the bottom activation of List() . I have used such an approach only for a specialized class of problems: enumeration of combinatorial objects (like graphs or designs) in a recursive implementation of backtracking. In such problems you are only interested in the object when it is completely finished, and all you want to do with it is count it, display it, or store it in a file. Moreover, during enumeration, there may be many false starts and the partially constructed objects need to be destroyed . Building the objects entirely on the stack relieves the programmer from dealing with these issues. However, I cannot imagine another class of problems where such an approach would be useful.

 // function List ----------------------------------    void List(PNODE tree,char* s,int& sp)    {      NODE n;      PNODE p;      n.value = Next(s,sp);      n.lch = n.rch = NULL;      if (tree == NULL)        tree = &n;      else{        p = tree;        while(1) {          if (n.value < p->value) {            if (p->lch == NULL) {              p->lch = &n;              break;            }else              p = p->lch;          }else{            if (p->rch == NULL) {              p->rch = &n;              break;            }else              p = p->rch;          }        }//endwhile      }      if (Next(s,sp) == -1) {  // we parsed the whole string        Show(tree);            // display the characters        putchar('\n');      }else        List(tree,s,sp);    }//end List 

The foregoing two examples serve as a reminder that linked data structures need not necessarily be linked through pointers, nor do they have to be completely built in dynamic memory. That being said, for the rest of this chapter we will assume the most common type of linked data structures: those built in dynamic memory and linked by pointers.

We have mentioned and illustrated the flexibility of linked data structures. One can easily add a piece, remove a piece, or reshuffle the pieces, for most of these activities require only some modifications of the links. But this "rubbery" nature of the links poses three major problems.

1. How can we move the whole structure to a different location in memory?

2. How can we record such a structure in a file and recreate it from the record?

3. How can we to transmit such a data structure across a communication link?

The first problem could be " solved " by simply recreating the structure and deleting the original one. But it would be impossible to control the placement of the new structure (except by using placement- new , if you were programming in C++). Nevertheless, such a solution would not work for problems 2 and 3. Possible solutions are compaction or serialization of the structure. By compaction we mean creating the data structure in a single contiguous segment of memory with a simultaneous "relativization" of addresses with respect to the beginning of the segment. By serialization we mean creating the data structure so that it consists of several compacted segments. For an illustration of serialization, take the tree we built in the three arrays value[] , lch[] , and rch[] . Ifwemove the arrays (which is easy to do - just copy their contents byte by byte to a new location) then at the target location we will find the tree intact. If we record the arrays in a file, byte by byte, then we can later read them byte by byte from the disk and recreate them - and thus the tree. Similarly, we can transmit each array byte by byte in a serial fashion across a communication channel, recreating the arrays (and hence the tree) on the recipient side. All these scenarios are plausible because the links are array indexes, and an array index is essentially a relative address with respect to the beginning of the array.

Our binary search tree is rather simple and so it was easy to build it already serialized, as we did in the three-arrays example. It would be more complicated for more complex structures; it may even be unfeasible to conceive of some data structures as serialized right from the beginning. Moreover, unless you really need to move, record and restore, or transmit the data structure, there is no need to embark on a complex serialization of the initial construction. We will discuss instead the taking of a given data structure and then compacting or serializing it.

Compaction requires the data structure to be stored in a single segment, so it would be possible to build the structure in compacted form only if we had a reasonable cap on its size before construction began . The appropriate raw memory segment could be allocated and forged into the data structure. Of course, we could embark upon dynamic extension of a given segment if more memory were needed, but that would slow processing and bring costs up significantly (since all the links must be updated when the segment is extended) and thus is not very practical. In contrast, for serialization we may have many segments as long as the addresses are properly relativized. This allows the building of serialized data structures directly and with little overhead.

The next example of serialization incorporates a strategy called memory allocation from a specific arena, which is implemented using the class-specific operators NODE::new and NODE::delete as well as overloads of the operators new and delete . Therefore, any dynamic object of class NODE is created by using the operator NODE::new and not the global one. The case is similar for destruction: we use the class-specific NODE::delete that does not do anything, for if we want to deallocate the memory then we will deallocate the whole arena. Note that each object of class NODE has a static item, ARENA* arena , a pointer to the arena assigned to the whole class. This is set by a public method TREE::SetArena() , which invokes a protected method NODE::SetArena() (it can do so because it is a "friend"). Each object of class TREE or class NODE points to the same object of class ARENA .

The arena allocates memory from segments - in our example, segments of an unreasonably small size of 24 bytes, a size chosen to force the arena to allocate several segments even for a small tree. The operator NODE::new uses the memory allocated from its arena. Thus, when a tree is created, it is built completely in several segments of the arena. Note that the arena can accommodate any allocation by dynamically creating more segments as needed. Even though the tree is stored in these segments, it is not serialized yet, for the addresses are still actual addresses and not relative to the beginning of each segment. The public method TREE::Relativize() starts a recursion of the protected method TREE::Relativize1() that replaces each address in the tree by a pair of two short integers: the first is the index of the segment the address happens to come from; the second is the offset from the beginning of the segment. For technical reasons the index of the segment is shifted upward by1, since otherwise the relativized address of the very first byte in the very first segment would be 0 (segment 0, byte 0) and then we could not tell a genuine NULL pointer from the one that pointed to the beginning of the arena before relativization. (Note that this did not bother us in the example of the tree stored in three arrays, for we were using null = -1 as a fake null "pointer".)

After relativization, the segments of the arena represent a serialized version of the tree. To illustrate this, in main() we make a copy of the arena ( b = arena; ) using the method ARENA::operator= (i.e., ARENA -specific assignment) and absolutize the addresses in the copy - a kind of reverse process to relativization, where each address interpreted as a pair ( segment +1, offset ) is replaced by the actual address. Using TREE::Show() on the re-created tree demonstrates that we indeed have the same tree. It is not hard to see that, had we stored the segments on a disk and then read them from the disk again (or transmitted them across a communication channel), after reassembling them and absolutizing the addresses we would have a perfect copy of the original linked tree.

The code presented next is simplified as much as possible in order to focus on allocation from arena and on relativization and absolutization of addresses. Hence all inessential checking is omitted, and the memory alignment is handled by passing the appropriate parameter to ARENA() during the instantiation (4 in our example) rather then being obtained for each platform in a more independent way.

 class ARENA { public:   ARENA(int ss,int a) {     arena = NULL;     last_segment = -1;     segment_size = ss;        //arena segment size     align = a;                //memory alignment boundary   }   ~ARENA() {     for(int i = 0; i <= last_segment; i++)      delete[] arena[i];     delete[] arena;   }   ARENA& operator= (const ARENA& ar) {     int i, j;     for(i=0; i <= last_segment; i++)  // destroy old data       delete[] arena[i];     delete[] arena;     arena = NULL;     segment_size = ar.segment_size;   // copy new data     next_ind = ar.next_ind;     last_segment = ar.last_segment;     align = ar.align;     arena = new char* [last_segment+1];     for(i = 0; i <= last_segment; i++) {       arena[i] = new char[segment_size];       for(j = 0; j < segment_size; j++)         arena[i][j] = ar.arena[i][j];     }     return *this;   }   void* Alloc(size_t s) { //alloc. memory of size s from its segment     char** a;             //obtains a new segment if need be     int i;     void* ret;     if (arena == NULL) {                       //alloc 1st segment       arena = new char*[1];       last_segment = 0;       arena[0] = new char[segment_size];       last_segment = 0;       next_ind = 0;     }else if (s > (size_t) segment_size-next_ind) {       last_segment++;       a = new char*[last_segment+1];       for(i = 0; i < last_segment; i++)         a[i] = arena[i];       delete[] arena;       arena = a;       arena[last_segment] = new char[segment_size];       next_ind = 0;     }     ret = (void*) &arena[last_segment][next_ind];     next_ind += s;     // align next_ind for future use     while(((long)&arena[last_segment][next_ind]%align)! = 0)       if (next_ind >= segment_size) break;     // if next_ind runs to the end of the segment, no problem     // on next Alloc() a new segment will be enforced     return ret;   } void* Relativize(void* s) {     //relativizes address s with respect     short segment, offset, *ip; //to the segment that s belongs to     void* res;     if (s == NULL) return NULL;     for(segment = 0; segment <= last_segment; segment++) {       if (s < arena[segment])         continue;       if (s >= arena[segment]+segment_size)         continue;       // so we have the right segment       offset = (short) ((long)s - (long)arena[segment]);       segment++;          // shift segment by 1 so the beginning       ip = (short*)&res;  // does not get relativized to NULL       *ip++ = segment;       *ip = offset;       return res;     }     return NULL;   } void* Absolutize(void* s) {  //absolutize relative address s     short *ip, segment, offset;     void* r;     if (s == NULL) return NULL;     r=s;     ip = (short*) &r;     segment = *ip++;     segment--;            // undo the shift     offset = *ip;     return (void*)&arena[segment][offset];   } protected:   char** arena;   short last_segment;   short segment_size;   short next_ind;   short align; };//end class ARENA class TREE; class NODE {   friend class TREE; public:   NODE() { value = 0; lch = rch = NULL; }   NODE(char c) { value = c; lch = rch = NULL; }   NODE& operator = (NODE& n) {     if (lch) delete lch;     if (rch) delete rch;     value = n.value;     lch = n.lch;     rch = n.rch;     arena = n.arena;     return *this;   } protected:   char value;   NODE *lch, *rch;   static ARENA *arena;   //the following methods are only for arena allocation   static void* operator new(size_t s) { return arena->Alloc(s); }   // we will deallocate the whole arena instead   static void operator delete(void* s) { return; }   static void SetArena(ARENA* a) { //set the arena for NODE object     static int first = 1;     if (first) {       arena = a;       first = 0;     }   } };//end class NODE ARENA* NODE::arena = NULL; class TREE { public:   TREE() { root = NULL; }   void Insert(char c) {  //start recursive insertion     NODE* p;     p = new NODE(c);     p->lch = NULL;     p->rch = NULL;     if (root == NULL) {       root = p;       return;     }else       Insert1(root,p);   }   void Show() {     if (root == NULL) return;     Show1(root);     cout << '\n' << flush;   }   void SetRoot(NODE* r) { root = r; }   NODE* GetRoot() { return root; }   static void SetArena(ARENA* a) {  //set arena for TREE object     static int first = 1;     if (first) {       arena = a;       NODE::SetArena(a);       first = 0;     }   }   void Relativize() {         //start recursive relativization     Relativize1(root);        //at the root     root = (NODE*)arena->Relativize(root);   }   void Absolutize() {         //start recursive absolutization                               //at the root     root = (NODE*)arena->Absolutize((void*)root);     Absolutize1(root);   } protected:   NODE* root;   static ARENA* arena; void Insert1(NODE* n,NODE* p) { //continue recursive insertion     if (p->value < n->value)        if (n->lch == NULL)          n->lch = p;        else          Insert1(n->lch,p);     else       if (n->rch == NULL)         n->rch = p;       else         Insert1(n->rch,p);   }   void Show1(NODE* p) {     if (p == NULL) return;     Show1(p->lch);     cout << ' ' << p->value;     Show1(p->rch);   }   void Relativize1(NODE* n) {  //continue recursive relativization     if (n == NULL) return;     Relativize1(n->lch);     Relativize1(n->rch);     n->lch = (NODE*)arena->Relativize((void*)n->lch);     n->rch = (NODE*)arena->Relativize((void*)n->rch);   }   void Absolutize1(NODE* n) {  //continue recursive absolutization     if (n == NULL) return;     n->lch = (NODE*)arena->Absolutize(n->lch);     n->rch = (NODE*)arena->Absolutize(n->rch);     Absolutize1(n->lch);     Absolutize1(n->rch);   } };//end class TREE ARENA* TREE::arena = NULL; // function main ----------------------------------------------- int main() {   ARENA arena(24,4), b(0,0);   TREE t, t1;   t.SetArena(&arena);   t.Insert('d');   t.Insert('c');   t.Insert('e');   t.Insert('a');   t.Insert('b');   t.Show();   t.Relativize();   b = arena;   t1.SetArena(&b);   t1.SetRoot(t.GetRoot());   t1.Absolutize();   t1.Show();   return 0; }//end main 

Let us now visualize the arena after each stage of the process. After node for 'd' is created:

After node for 'c' is created:

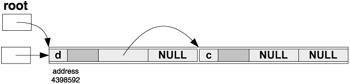
After node for 'e' is created:

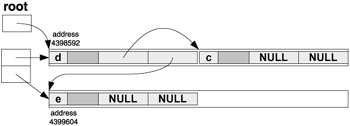
After node for 'a' is created:

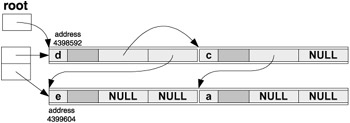
And finally, after the last node for 'b' is created:

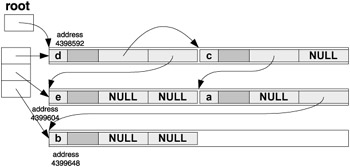
This clearly shows how the arena allocation keeps the tree quite "compact", even though it is a fully linked data structure and all pointers hold actual addresses.

In the following diagram we indicate the relativized addresses as pairs of ( segment +1, offset ) values. The tree is relativized:

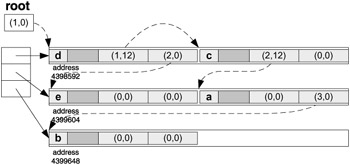
The arena is copied into a different location. The data kept in the arena (and so the relativized tree) is the same as in the original one:

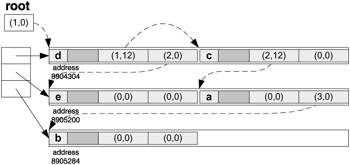
The addresses are absolutized and the tree "pops out" again:

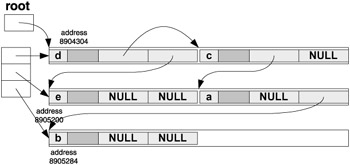
If we had known the size of the tree before we created it (it is 60 bytes including padding), then we might have initialized the arena as ARENA arena(60,4) and stored the tree in a single segment; in fact, we would have compacted it. Another possibility for compacting the tree would be to create it normally (without arena allocation), count its size, and make a copy using arena allocation to fit it into a single segment. Note that, with a single segment, the relativized addresses are actually just offsets from the beginning of the segment. This is not hard to do, since the code for TREE and NODE will work perfectly well if we just omit references to the arena there and in the overloaded new and delete . But it may be complicated to establish the size of an existing tree that includes padding, since the size may depend on such elusive aspects as the order in which items are defined. The only reasonable approach to counting the size of a linked data structure is doing so during construction - allocate some memory and add it to the count.

Our approach to serialization preserves padding. This may or may not be desirable. If we preserve padding then all the items remain "justified" and hence can be accessed (before relativization and after absolutization) in the normal way; for instance, the usual pointer notation works correctly. If we intend to move the data structure (either via a disk or across a communication channel) to a different platform, then there is no reason to preserve the padding and transmit all that junk. We could compact the tree without the padding, but then we might not be able to use the convenient pointer or membership notation for accessing the individual items.

We deliberately designed the structure/class NODE so that it has size of 12 bytes, but 3 bytes are wasted on padding (see Figure 9.1). If we compact it without the padding then the space is saved - but now we cannot use p->lch or p->rch to refer to the pointers to the child nodes; see Figure 9.2.

Figure 9.1: A node with 'a' stored in it

Figure 9.2: A compacted node with 'a' stored in it

In order to work with such a compacted structure, we must have our own custom-made functions for accessing items that are not properly aligned. The following example creates a regular tree, computes its size without padding, and creates a compacted version of the tree that can only be accessed using the specialized access functions; then the compacted version is relativized. The resulting relativized compacted version can be transferred to a machine with a different memory alignment, absolutized, and accessed by again using the specialized access functions. For the sake of simplicity we have omitted the code dealing with different "endianess" (see Chapter 3). Class NODE remains the same as before.

 class TREE { public:   TREE() { root = NULL; }   void Insert(char c) {     NODE* p;     p = new NODE(c);     p->lch = NULL;     p->rch = NULL;     if (root == NULL) {       root = p;       return;     }else       Insert1(root,p);   }   void Show() {     if (root == NULL) return;     Show1(root);     cout << '\n'<< flush;   }   int Size() {     return Size1(root);   }   char* Compact(char*& croot) {     char* segment;     int ind = 0;     segment = (char*) new char[Size()];     croot = Compact1(ind,segment,root);     return segment;   }   void CShow(char* segment,char* cnode) {     if (cnode == NULL) return;     CShow(segment,GetLch(cnode));     cout << ' ' << GetValue(cnode);     CShow(segment,GetRch(cnode));   }   char* Relativize(char* segment,char* croot) {     char* p; if (croot == NULL) return NULL; p = GetLch(croot); if (p != NULL) { Relativize1(segment,p); PutLch(croot,(char*)(p-segment+1)); // shift by 1 to // distinguish from NULL } p = GetRch(croot); if (p != NULL) { Relativize1(segment,p); PutRch(croot,(char*)(p-segment+1)); // shift by 1 to                                     // distinguish from NULL } return ((char*)(croot-segment+1));  // shift by 1 to                                     // distinguish from NULL } char* Absolutize(char* segment,char* croot) { if (croot == NULL) return NULL; // undo the shift croot = ((char*)(segment+((unsigned long)croot)-1)); Absolutize1(segment,croot); return croot;   } protected:   NODE* root;   void Insert1(NODE* n,NODE* p) {     if (p->value < n->value)       if (n->lch == NULL)         n->lch = p;       else         Insert1(n->lch,p);       else         if (n->rch == NULL)           n->rch = p;         else           Insert1(n->rch,p);   }   void Show1(NODE* p) {     if (p == NULL) return;     Show1(p->lch);     cout << ' ' << p->value;     Show1(p->rch);   }   int Size1(NODE* p) {     if (p == NULL)       return 0;     return p->Size()+Size1(p->lch)+Size1(p->rch);   }   char GetValue(char* p) { // use instead of p->value     return *p;   }   void PutValue(char* p,char c) { // use instead of p->value     *p=c;   }   char* GetLch(char* p) {  // use instead of p->lch     char *q, *q1, *q2;     int i;     q2 = (char*)&q;     q1 = p+sizeof(char);     for(i = 0; i < sizeof(char*); i++)       *q2++ = *q1++;     return q;   }   void PutLch(char* p,char* addr) {  // use instead of p->lch     char *q, *q1, *q2;     int i;     q = addr;     q2 = (char*)&q;     q1 = p+sizeof(char);     for(i = 0; i < sizeof(char*); i++)       *q1++ = *q2++;   }   char* GetRch(char* p) {  // use instead of p->rch     char *q, *q1, *q2;     int i;     q2 = (char*)&q;     q1 = p+sizeof(char)+sizeof(char*);     for(i = 0; i < sizeof(char*); i++)       *q2++ = *q1++;     return q;   } void PutRch(char* p,char* addr) {  // use instead of p->rch   char *q, *q1, *q2;   int i;   q = addr;   q2 = (char*)&q;   q1 = p+sizeof(char)+sizeof(char*);   for(i = 0; i < sizeof(char*); i++)     *q1++ = *q2++; } char* Compact1(int& ind,char* segment,NODE* n) {   char *lch, *rch, *ret;   if (n == NULL) return NULL;   lch = Compact1(ind,segment,n->lch);   rch = Compact1(ind,segment,n->rch);   //copy n to segment to location segment[ind]   ret = &segment[ind];   PutValue(&segment[ind],n->value);   PutLch(&segment[ind],lch);   PutRch(&segment[ind],rch);   ind += n->Size();   return ret; } void Relativize1(char* segment,char* cnode) {   char* p;   p = GetLch(cnode);   if (p != NULL) {     Relativize1(segment,p);     PutLch(cnode,(char*)(p-segment+1)); // shift up by 1 to                                         // distinguish from NULL   }   p = GetRch(cnode);   if (p != NULL) {     Relativize1(segment,p);     PutRch(cnode,(char*)(p-segment+1)); // shift up by 1 to                                         // distinguish from NULL   } } void Absolutize1(char* segment,char* cnode) {   char* p;   if ((p = GetLch(cnode)) != NULL) {     // undo the shift     p = ((char*)(segment+((unsigned long)p)-1));     PutLch(cnode,p);     Absolutize1(segment,p);   }   if ((p = GetRch(cnode)) != NULL) {     // undo the shift     p = ((char*)(segment+((unsigned long)p)-1));     PutRch(cnode,p);     Absolutize1(segment,p);   } } };//end class TREE 

After a tree is built in the normal way, it can be compacted using croot = Compact(segment,croot) . Note that char* croot must be initialized to NULL prior to the call. The function Compact() will allocate a contiguous segment of the correct size, will make segment point to it, and will then store the tree in a compacted form; it also returns a pointer to the root, which need not be the very first node in the segment. The compacted tree cannot be accessed normally, but it can be viewed using CShow() - show compacted tree. We can then relativize it, absolutize it, and show it again using CShow() to verify that the program has worked properly. Again, we must ensure that a genuine NULL pointer can be distinguished from the very first byte in the segment.

In Figure 9.3, the compacted tree (as built and compacted in the previous example) is shown. Figure 9.4 illustrates the compacted tree after relativization.

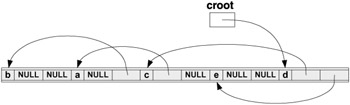
Figure 9.3: Compacted tree from the example

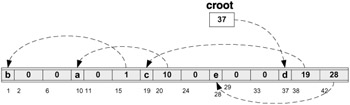
Figure 9.4: Compacted tree from the example ” after relativization

It is clear that many other methods could be used to serialize or compact linked data structures. In real life, an ad hoc method pertinent to a particular structure is normally used. However, in this chapter we have tried to provide some insight into the issues and furnish the reader with some ideas of how to go about resolving them. In our age of networking and distributed computing, moving data structures among different machines and different platforms is fast becoming commonplace.

Allocation from a specific arena can be used for problems other than serializing linked data structures. Any application that needs to perform a lot of allocation/deallocation of small chunks of memory may have its performance dramatically improved if the allocation is handled through a specific arena. Some authors claim that the time spent by a running program on allocation and deallocation is by far the most significant component in overall performance, so any improvement in these functions should yield welcome dividends .