Some Simple Uses for Trigonometric Functions
| | | ||||||||||||||||||||||||
| ||||
| | ||||
Skinned Surfaces
A skinned surface is very similar to a swept surface. The difference is that the skinned surface correctly accounts for bends in the path curve. Figure 10.9 features the same path and cross section shown in Figure 10.8, only now the resulting surface is a skinned surface.
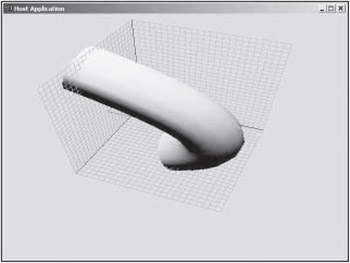
Figure 10.9: Skinned surface instead of a swept surface.
The basic code for the skinned surface is identical to swept surfaces in terms of how the NURBS calculations are carried out. The differences occur after all the NURBS calculations. The skinning portion involves a fair amount of vector calculations.
To understand the calculations, first consider the cross section curve. In the samples, the curve is constructed on the xz plane. This is not a requirement, but it does make things a little easier to visualize. You could define the cross section with whatever orientation you want (by moving the control points). The math will work out the same as long as you are consistent. If you think of the shape as lying on a plane, you can think of a normal vector to that plane as shown in Figure 10.10.
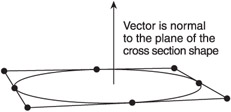
Figure 10.10: Cross section and normal vector.
As the path bends, you want the cross section to rotate accordingly . In effect, you want the normal of the cross section to match the tangent of the path curve, as shown in Figure 10.11.
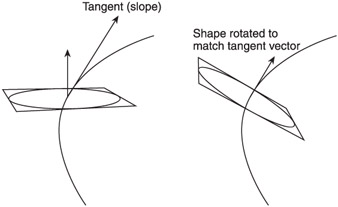
Figure 10.11: Rotating the cross section to match the tangent to the path.
So, you have two vectors and you want to rotate one to match the other. This can be done fairly easily with the dot product and cross product. The cross product of any two vectors produces a third vector that is perpendicular to both. This will serve as an axis of rotation. In Figure 10.11, the axis is either into or out of the page (depending on how you order the cross product). If you rotate the cross section normal vector around that axis, you will eventually match the tangent vector.
The angle of the rotation is given by the dot product. The dot product of two normalized vectors yields the cosine of the angle between those vectors. The arccosine gives you the angle value. Once you know the angle and the axis, you can rotate the cross section to match the tangent. Figure 10.12 shows how all the steps fit together.
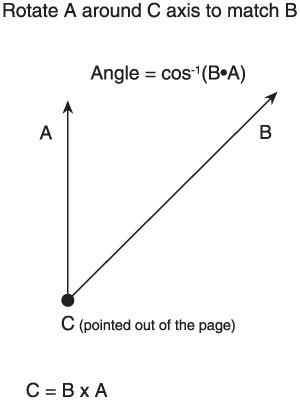
Figure 10.12: Rotating one vector to match another.
The code for this is straightforward. You have most of the pieces already. First, there is one difference in the position calculations. Instead of adding the u and v components together, the cross section shape is computed along with an offset value as shown next .
pVertices[Current].x += (NumeratorU * pVertices[ControlIndexU].x / DenominatorU);
VOffset.x += (NumeratorV * pVertices[ControlIndexV].x / DenominatorV); pVertices[Current].y += (NumeratorU * pVertices[ControlIndexU].y / DenominatorU); VOffset.y += (NumeratorV * pVertices[ControlIndexV].y / DenominatorV); pVertices[Current].z += (NumeratorU * pVertices[ControlIndexU].z / DenominatorU); VOffset.z += (NumeratorV * pVertices[ControlIndexV].z / DenominatorV);
The tangent vector for the path is dP/dV-the slope value that I have been calculating all along. Between the offset value and the tangent vector, you have everything you need to "skin" the surface. First, create a translation matrix. This will offset the cross section as you saw with swept surfaces. The reason for the matrix is that matrix transformations are order dependent. You need to offset the cross section after you rotate it.
D3DXMATRIX Translation; D3DXMatrixTranslation(&Translation, VOffset.x, VOffset.y, VOffset.z);
I define a rotation matrix, an axis vector, and a base direction. The base direction is the normal vector of the cross section and I chose these values based on the fact that my shape is defined on the xz plane. If you choose to define the cross section differently, you will need to change the values. Also, note that both the base direction vector and the dPdV vector are normalized at this point.
D3DXMATRIX Rotation; D3DXVECTOR3 Axis; D3DXVECTOR3 BaseDirection(0.0f, 1.0f, 0.0f);
The angle value is the arccosine of the dot product of the two vectors. The axis of rotation is given by the cross product.
float Angle = acos(D3DXVec3Dot(&BaseDirection, &dPdV)); D3DXVec3Cross(&Axis, &BaseDirection, &dPdV);
The D3DX library provides a convenient function to create a rotation matrix from an angle and an axis of rotation. This gives you the rotation matrix:
D3DXMatrixRotationAxis(&Rotation, &Axis, Angle);
The D3DX library also provides an easy way to transform a point with a matrix. Here, I concatenate the translation and rotation matrices and use them to transform the vertex position.
D3DXVec3TransformCoord((D3DXVECTOR3 *)&(pVertices[Current]), (D3DXVECTOR3 *)&(pVertices[Current]), &(Rotation * Translation));
The result is a vertex on a skinned surface as shown in Figure 10.9. These simple bent cylinders are starting to look as boring as the rubber sheet examples, so I also provided a sample that uses skinned surfaces to model a spring, as shown in Figure 10.13.
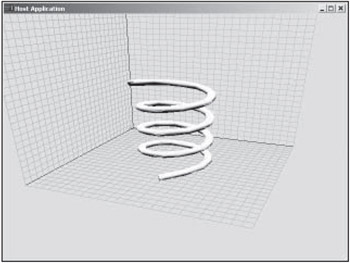
Figure 10.13: A skinned spring.
The code for the spring is also on the CD. Basically, I defined a helical path shape and a circular cross section. After that, the code is exactly the same as any other skinned surface. This can be interesting because you can begin to think about higher-level parametric shapes . For instance, you could easily write a function that produces any type of spring based on a diameter, a height, number of turns, and level of detail. The resulting mesh can be easily generated with the now familiar NURBS calculations.
| | ||||
| ||||
| | ||||
EAN: 2147483647
Pages: 104