Part Two: Focus on Curves

Defining Sine, Cosine, and Tangent

Note 

Remember that all trigonometric functions take parameters measured in radians. If you are measuring angles in degrees, you may need to convert your units before passing them to the trigonometric functions. Remember that 360 degrees equals 2pi radians. Having said that, I will use degrees for many of my explanations simply because most people seem to think in degrees.

Trigonometry is the branch of mathematics that helps us understand angular relationships between the sides of triangles. Trigonometric functions are tools you can use to relate angles to distances and vice versa. Geometrically, these functions are based on the properties of a right triangle. In this chapter, I will concentrate on the three basic trigonometric functions: sine, cosine, and tangent. There are more, but these first three are the most useful for basic tasks . These functions are easy to understand if you begin by looking at a series of right triangles inscribed in a circle, as shown in Figure 2.1.

Figure 2.1: Triangles inscribed in a circle.

Each of the circles has a radius of r. Angles about the center of the circle are not measured in degrees. Instead, a full circle is 2pi radians.

As you can see, the lengths of the sides of each triangle change as the angles change. The three trigonometric functions are based on these changes. As Figure 2.1 shows, each side of the triangle can be defined relative to the angle. The sides are the hypotenuse , the adjacent side, and the opposite side. Sine, cosine, and tangent are defined as ratios of the lengths of those sides for any angle, as shown in the following equations.

(2.1) Sine, cosine, and tangent.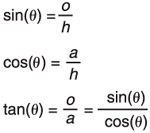 

Note that on a unit circle (with a radius of 1.0), the ratios for sine and cosine are equal to the lengths of the opposite and adjacent sides respectively. All of the rest of the graphs in this chapter assume a unit circle. Tangent is a little different. It defines the ratio of the opposite and adjacent side. This is equivalent to the "rise over run" definition of the slope of a line. Therefore, tangent is the slope of the hypotenuse. A line that is tangent to a curve at a given point has the same slope as the slope of the curve at that point.

If you sketch out a few triangles like those shown in Figure 2.1, you'll see that the opposite and adjacent sides lengthen and shorten as the angle grows. Equation 2.1 shows that the lengths can be described by sine and cosine. Therefore, you can see exactly how the lengths change by graphing sine and cosine as shown in Figure 2.2. Note that the x-axis is now the angle theta, given in radians.

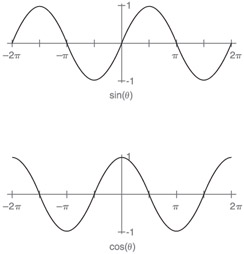
Figure 2.2: Graphs of sine and cosine.

The graphs are both the same shape, but they are offset by 90 degrees (pi/2 radians). This should come as no surprise. Sine basically gives you a vertical measurement. Cosine gives you a horizontal measurement. You can turn one into the other if you rotate the circle by pi/2 radians. I will address this later when I talk about phase.

Tangent is different. If you think of tangent as the slope of the hypotenuse, you can see that the slope changes from zero to infinity over the first 90 degrees. It then switches to negative infinity and back to zero over the second 90 degrees. Figure 2.3 shows a graph of the tangent function.

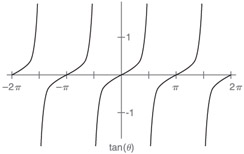
Figure 2.3: Graph of tangent.

Figures 2.2 and 2.3 demonstrate the fact that these functions are periodic. This means that they repeat a specific pattern over specific time intervals (periods). Figure 2.4 shows one cycle of a sine wave. Its period is 2pi radians.

Figure 2.4: One cycle of a sine wave.

Sine, cosine, and tangent are useful functions for dealing with angles, but the sine wave pattern is useful simply by virtue of its shape and periodicity. Sine in particular is nice because each cycle of the wave oscillates between -1 and 1. In the next section, I will define the properties of a wave and discuss how they can be useful.