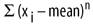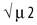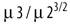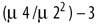Computing Variance, Standard Deviation, and Other Statistical Functions
Problem
You want to compute one or more of the common statistics such as variance, standard deviation, skew, and kurtosis of a sequence of numbers.
Solution
You can use the accumulate function from the header to compute many meaningful statistical functions beyond simply the sum by passing custom function objects. Example 11-9 shows how to compute several important statistical functions, using accumulate.
Example 11-9. Statistical functions
#include
#include
#include
#include
#include
#include
using namespace std;
template
T nthPower(T x) {
T ret = x;
for (int i=1; i < N; ++i) {
ret *= x;
}
return ret;
}
template
struct SumDiffNthPower {
SumDiffNthPower(T x) : mean_(x) { };
T operator( )(T sum, T current) {
return sum + nthPower(current - mean_);
}
T mean_;
};
template
T nthMoment(Iter_T first, Iter_T last, T mean) {
size_t cnt = distance(first, last);
return accumulate(first, last, T( ), SumDiffNthPower(mean)) / cnt;
}
template
T computeVariance(Iter_T first, Iter_T last, T mean) {
return nthMoment(first, last, mean);
}
template
T computeStdDev(Iter_T first, Iter_T last, T mean) {
return sqrt(computeVariance(first, last, mean));
}
template
T computeSkew(Iter_T begin, Iter_T end, T mean) {
T m3 = nthMoment(begin, end, mean);
T m2 = nthMoment(begin, end, mean);
return m3 / (m2 * sqrt(m2));
}
template
T computeKurtosisExcess(Iter_T begin, Iter_T end, T mean) {
T m4 = nthMoment(begin, end, mean);
T m2 = nthMoment(begin, end, mean);
return m4 / (m2 * m2) - 3;
}
template
void computeStats(Iter_T first, Iter_T last, T& sum, T& mean,
T& var, T& std_dev, T& skew, T& kurt)
{
size_t cnt = distance(first, last);
sum = accumulate(first, last, T( ));
mean = sum / cnt;
var = computeVariance(first, last, mean);
std_dev = sqrt(var);
skew = computeSkew(first, last, mean);
kurt = computeKurtosisExcess(first, last, mean);
}
int main( )
{
vector v;
v.push_back(2);
v.push_back(4);
v.push_back(8);
v.push_back(10);
v.push_back(99);
v.push_back(1);
double sum, mean, var, dev, skew, kurt;
computeStats(v.begin( ), v.end( ), sum, mean, var, dev, skew, kurt);
cout << "count = " << v.size( ) << "
";
cout << "sum = " << sum << "
";
cout << "mean = " << mean << "
";
cout << "variance = " << var << "
";
cout << "standard deviation = " << dev << "
";
cout << "skew = " << skew << "
";
cout << "kurtosis excess = " << kurt << "
";
cout << endl;
}
The program in Example 11-9 produces the following output:
count = 6 sum = 124 mean = 20.6667 variance = 1237.22 standard deviation = 35.1742 skew = 1.75664 kurtosis excess = 1.14171
Discussion
Some of the most important statistical functions (e.g., variance, standard deviation, skew, and kurtosis) are defined in terms of standardized sample moments about the mean. The precise definitions of statistical functions vary somewhat from text to text. This text uses the unbiased definitions of the statistical functions shown in Table 11-1.
|
Statistical function |
Equation |
|---|---|
|
nth central moment ( |
|
|
Variance |
|
|
Standard deviation |
|
|
Skew |
|
|
Kurtosis excess |
|
|
The simplest way to code the statistical functions is to define them all in terms of moments. Since there are several different moments used, each one accepting a constant integer value, I pass the constant as a template parameter. This allows the compiler to potentially generate more efficient code because the integer is known at compile time.
The moment function is defined using the mathematical summation operator . Whenever you think of the summation operation you should think of the accumulate function from the header. The accumulate function has two forms: one accumulates using operator+ and the other uses an accumulator functor that you need to provide. Your accumulator functor will accept two values: the accumulated value so far, and the value at a specific position in the sequence.
Example 11-10 illustrates how accumulate works by showing how the user supplied functor is called repeatedly for each element in a series.
Example 11-10. Sample implementation of accumulate
template
Iter_T accumulate(Iter_T begin, Iter_T end, Value_T value, BinOp_T op) {
while (begin != end) {
value = op(value, *begin++)
}
return value;
}
Building C++ Applications
- Introduction to Building
- Obtaining and Installing GCC
- Building a Simple Hello, World Application from the Command Line
- Building a Static Library from the Command Line
- Building a Dynamic Library from the Command Line
- Building a Complex Application from the Command Line
- Installing Boost.Build
- Building a Simple Hello, World Application Using Boost.Build
- Building a Static Library Using Boost.Build
- Building a Dynamic Library Using Boost.Build
- Building a Complex application Using Boost.Build
- Building a Static Library with an IDE
- Building a Dynamic Library with an IDE
- Building a Complex Application with an IDE
- Obtaining GNU make
- Building A Simple Hello, World Application with GNU make
- Building a Static Library with GNU Make
- Building a Dynamic Library with GNU Make
- Building a Complex Application with GNU make
- Defining a Macro
- Specifying a Command-Line Option from Your IDE
- Producing a Debug Build
- Producing a Release Build
- Specifying a Runtime Library Variant
- Enforcing Strict Conformance to the C++ Standard
- Causing a Source File to Be Linked Automatically Against a Specified Library
- Using Exported Templates
Code Organization
- Introduction
- Making Sure a Header File Gets Included Only Once
- Ensuring You Have Only One Instance of a Variable Across Multiple Source Files
- Reducing #includes with Forward Class Declarations
- Preventing Name Collisions with Namespaces
- Including an Inline File
Numbers
- Numbers
- Introduction
- Converting a String to a Numeric Type
- Converting Numbers to Strings
- Testing Whether a String Contains a Valid Number
- Comparing Floating-Point Numbers with Bounded Accuracy
- Parsing a String Containing a Number in Scientific Notation
- Converting Between Numeric Types
- Getting the Minimum and Maximum Values for a Numeric Type
Strings and Text
- Strings and Text
- Introduction
- Padding a String
- Trimming a String
- Storing Strings in a Sequence
- Getting the Length of a String
- Reversing a String
- Splitting a String
- Tokenizing a String
- Joining a Sequence of Strings
- Finding Things in Strings
- Finding the nth Instance of a Substring
- Removing a Substring from a String
- Converting a String to Lower- or Uppercase
- Doing a Case-Insensitive String Comparison
- Doing a Case-Insensitive String Search
- Converting Between Tabs and Spaces in a Text File
- Wrapping Lines in a Text File
- Counting the Number of Characters, Words, and Lines in a Text File
- Counting Instances of Each Word in a Text File
- Add Margins to a Text File
- Justify a Text File
- Squeeze Whitespace to Single Spaces in a Text File
- Autocorrect Text as a Buffer Changes
- Reading a Comma-Separated Text File
- Using Regular Expressions to Split a String
Dates and Times
- Dates and Times
- Introduction
- Obtaining the Current Date and Time
- Formatting a Date/Time as a String
- Performing Date and Time Arithmetic
- Converting Between Time Zones
- Determining a Days Number Within a Given Year
- Defining Constrained Value Types
Managing Data with Containers
- Managing Data with Containers
- Introduction
- Using vectors Instead of Arrays
- Using vectors Efficiently
- Copying a vector
- Storing Pointers in a vector
- Storing Objects in a list
- Mapping strings to Other Things
- Using Hashed Containers
- Storing Objects in Sorted Order
- Storing Containers in Containers
Algorithms
- Algorithms
- Introduction
- Iterating Through a Container
- Removing Objects from a Container
- Randomly Shuffling Data
- Comparing Ranges
- Merging Data
- Sorting a Range
- Partitioning a Range
- Performing Set Operations on Sequences
- Transforming Elements in a Sequence
- Writing Your Own Algorithm
- Printing a Range to a Stream
Classes
- Classes
- Introduction
- Initializing Class Member Variables
- Using a Function to Create Objects (a.k.a. Factory Pattern)
- Using Constructors and Destructors to Manage Resources (or RAII)
- Automatically Adding New Class Instances to a Container
- Ensuring a Single Copy of a Member Variable
- Determining an Objects Type at Runtime
- Determining if One Objects Class Is a Subclass of Another
- Giving Each Instance of a Class a Unique Identifier
- Creating a Singleton Class
- Creating an Interface with an Abstract Base Class
- Writing a Class Template
- Writing a Member Function Template
- Overloading the Increment and Decrement Operators
- Overloading Arithmetic and Assignment Operators for Intuitive Class Behavior
- Calling a Superclass Virtual Function
Exceptions and Safety
- Exceptions and Safety
- Introduction
- Creating an Exception Class
- Making a Constructor Exception-Safe
- Making an Initializer List Exception-Safe
- Making Member Functions Exception-Safe
- Safely Copying an Object
Streams and Files
- Streams and Files
- Introduction
- Lining Up Text Output
- Formatting Floating-Point Output
- Writing Your Own Stream Manipulators
- Making a Class Writable to a Stream
- Making a Class Readable from a Stream
- Getting Information About a File
- Copying a File
- Deleting or Renaming a File
- Creating a Temporary Filename and File
- Creating a Directory
- Removing a Directory
- Reading the Contents of a Directory
- Extracting a File Extension from a String
- Extracting a Filename from a Full Path
- Extracting a Path from a Full Path and Filename
- Replacing a File Extension
- Combining Two Paths into a Single Path
Science and Mathematics
- Science and Mathematics
- Introduction
- Computing the Number of Elements in a Container
- Finding the Greatest or Least Value in a Container
- Computing the Sum and Mean of Elements in a Container
- Filtering Values Outside a Given Range
- Computing Variance, Standard Deviation, and Other Statistical Functions
- Generating Random Numbers
- Initializing a Container with Random Numbers
- Representing a Dynamically Sized Numerical Vector
- Representing a Fixed-Size Numerical Vector
- Computing a Dot Product
- Computing the Norm of a Vector
- Computing the Distance Between Two Vectors
- Implementing a Stride Iterator
- Implementing a Dynamically Sized Matrix
- Implementing a Constant-Sized Matrix
- Multiplying Matricies
- Computing the Fast Fourier Transform
- Working with Polar Coordinates
- Performing Arithmetic on Bitsets
- Representing Large Fixed-Width Integers
- Implementing Fixed-Point Numbers
Multithreading
- Multithreading
- Introduction
- Creating a Thread
- Making a Resource Thread-Safe
- Notifying One Thread from Another
- Initializing Shared Resources Once
- Passing an Argument to a Thread Function
Internationalization
- Internationalization
- Introduction
- Hardcoding a Unicode String
- Writing and Reading Numbers
- Writing and Reading Dates and Times
- Writing and Reading Currency
- Sorting Localized Strings
XML
- XML
- Introduction
- Parsing a Simple XML Document
- Working with Xerces Strings
- Parsing a Complex XML Document
- Manipulating an XML Document
- Validating an XML Document with a DTD
- Validating an XML Document with a Schema
- Transforming an XML Document with XSLT
- Evaluating an XPath Expression
- Using XML to Save and Restore a Collection of Objects
Miscellaneous
- Miscellaneous
- Introduction
- Using Function Pointers for Callbacks
- Using Pointers to Class Members
- Ensuring That a Function Doesnt Modify an Argument
- Ensuring That a Member Function Doesnt Modify Its Object
- Writing an Operator That Isnt a Member Function
- Initializing a Sequence with Comma-Separated Values
Index
EAN: 2147483647
Pages: 241
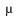 n)
n)