4.4 Random Variables

Suppose that a coin is tossed five times. What is the total number of heads? This quantity is what has traditionally been called a random variable. Intuitively, it is a variable because its value varies, depending on the actual sequence of coin tosses; the adjective "random" is intended to emphasize the fact that its value is (in a certain sense) unpredictable. Formally, however, a random variable is neither random nor a variable.

Definition 4.4.1

A random variable X on a sample space (set of possible worlds) W is a function from W to some range. A gamble is a random variable whose range is the reals.

Example 4.4.2

If a coin is tossed five times, the set of possible worlds can be identified with the set of 2⁵ sequences of five coin tosses. Let NH be the gamble that corresponds to the number of heads in the sequence. In the world httth, where the first and last coin tosses land heads and the middle three land tails, NH(httth) = 2: there are two heads. Similarly, NH(ththt) = 2 and NH(ttttt) = 0.

What is the probability of getting three heads in a sequence of five coin tosses? That is, what is the probability that NH = 3? Typically this is denoted μ(NH = 3). But probability is defined on events (i.e., sets of worlds), not on possible values of random variables. NH = 3 can be viewed as shorthand for a set of worlds, namely, the set of worlds where the random variable NH has value 3; that is, NH = 3 is shorthand for {w : NH(w) = 3}. More generally, if X is a random variable on W one of whose possible values is x, then X = x is shorthand for {w : X(w) = x} and μ(X = x) can be viewed as the probability that X takes on value x.

So why are random variables of interest? For many reasons. One is that they play a key role in the definition of expectation; see Chapter 5. Another, which is the focus of this chapter, is that they provide a tool for structuring worlds. The key point here is that a world can often be completely characterized by the values taken on by a number of random variables. If a coin is tossed five times, then a possible world can be characterized by a 5-tuple describing the outcome of each of the coin tosses. There are five random variables in this case, say X₁, …, X₅, where X_i describes the outcome of the ith coin tosses.

This way of describing a world becomes particularly useful when one more ingredient is added: the idea of talking about independence for random variables. Two random variables X and Y are independent if learning the value of one gives no information about the value of the other. For example, if a fair coin is tossed ten times, the number of heads in the first five tosses is independent of the number of heads in the second five tosses.

Definition 4.4.3

Let (X denote the set of possible values (i.e., the range) of the random variable X. Random variables X and Y are (probabilistically) conditionally independent given Z (with respect to probability measure μ) if, for all x ∊ (X), and y ∊ (Y), and z ∊ (Z), the event X = x is conditionally independent of Y = y given Z = z. More generally, if X ={X₁, …, X_n}, Y ={Y₁, …, Y_m}, and Z ={Z₁, …, Z_k} are sets of random variables, then X and Y are conditionally independent given Z (with respect to μ), written I^rv_μ(X, Y | Z), if X₁ = x₁ ∩ … ∩ X_n = x_n is conditionally independent of Y₁ = y₁ ∩ … ∩ Y_m = y_m given Z₁ = z₁ ∩ … ∩ Z_k = z_k for all x_i ∊ (X_i), i =1, …, n, y_j ∊ (Y_j), j = 1,…, m, and z_h ∊ (Z_h), h = 1, …,k. (If Z = ∅, then I^rv_μ(X, Y | Z) if X and Y are unconditionally independent, that is, if I^rv_μ(X = x, Y = x | W) for all x, y. If either X ≠ ∅ or Y = ∅, then I^rv_μ(X, Y | Z) is taken to be vacuously true.)

I stress that, in this definition, X = x, Y = y, and Z = z represent events (i.e., subsets of W, the set of possible worlds), so it makes sense to intersect them.

The following result collects some properties of conditional independence for random variables:

Theorem 4.4.4

For all probability measures μ on W, the following properties hold for all sets X, Y, Y′, and Z of random variables on W :

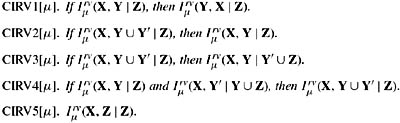
Proof See Exercise 4.14.

Again, I omit the parenthetical μ when it is clear from context or plays no significant role. Clearly, CIRV1 is the analogue of the symmetry property CI1. Properties CIRV2– 5 have no analogue among CI1–5. They make heavy use of the fact that independence between random variables means independence of the events that result from every possible setting of the random variables. CIRV2 says that if, for every setting of the values of the random variables in Z, the values of the variables in X are unrelated to the values of the variables in Y ∪ Y′, then surely they are also unrelated to the values of the variables in Y. CIRV3 says that if X and Y ∪ Y′ are independent given Z—which implies, by CIRV2, that X and Y are independent given Z—then X and Y remain independent given Z and the (intuitively irrelevant) information in Y′. CIRV4 says that if X and Y are independent given Z, and X and Y′ are independent given Z and Y, then X must have been independent of Y ∪ Y′ (given Z) all along. Finally, CIRV5 is equivalent to the collection of statements I_μ(X = x, Z = z | Z = z′), for all x ∊ (X) and z, z′ ∊ (Z), each of which can easily be shown to follow from CI2, CI3, and CI5.

CIRV1–5 are purely qualitative properties of conditional independence for random variables, just as CI1–5 are qualitative properties of conditional independence for events. It is easy to define notions of conditional independence for random variables with respect to the other notions of uncertainty considered in this book. Just as with CI1–5, it then seems reasonable to examine whether CIRV1–5 hold for these definitions (and to use them as guides in constructing the definitions). It is immediate from the symmetry imposed by the definition of conditional independence that CIRV1[Pl] for all conditional plausibility measures Pl. It is also easy to show that CIRV5[Pl] holds for all cpms Pl (Exercise 4.15). On the other hand, it is not hard to find counterexamples showing that CIRV2–4 do not hold in general (see Exercises 4.16 and 4.17). However, CIRV1–5 do hold for all algebraic cps's. Thus, the following result generalizes Theorem 4.4.4 and makes it clear that what is really needed for CIRV1–5 are the algebraic properties Alg1–4.

Theorem 4.4.5

If (W, , ′, Pl) is an algebraic cps, then CIRV1[Pl]–CIRV5[Pl] hold.

Proof See Exercise 4.19.

It is immediate from Proposition 3.9.2 and Theorem 4.4.5 that CIRV1–5 holds for ranking functions, possibility measures (with both notions of conditioning), and sets P of probability measures represented by the plausibility measure Pl_퓹.