Exercises
|
-
11.1 Show that if both 풯 and 풯′ contain all the symbols that appear in φ and KB, then
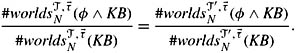
-
11.2 Let φ= be the result of replacing all instances of approximate equality and approximate inequality (i.e., ≈i, ≼i, and ≽i, for any i)in φ by equality and inequality (=, ≤, and ≥, respectively). Show that
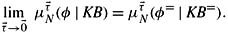
Thus, if the order of the limits in the definition of μ∞(φ | KB) were reversed, then all the advantages of using approximate equality would be lost.
-
11.3 Show that unless
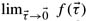 is independent of how
is independent of how 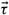 approaches
approaches 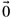 , there will be some way of having
, there will be some way of having 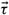 approach
approach 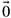 for which the limit does not exist at all.
for which the limit does not exist at all. -
11.4 Show that if a0, a1, … is a sequence of real numbers bounded from below, then lim infn→∞ an exists. Similarly, show that if a0, a1, … is bounded from above, then lim supn→∞ an exists. (You may use the fact that a bounded increasing sequence of real numbers has a limit.)
-
11.5 Show that, in the proof of Theorem 11.3.2,
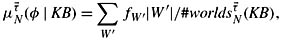
where the sum is taken over all clusters W′.
-
*11.6 Theorem 11.3.2 can be generalized in several ways. In particular,
-
it can be applied to more than one individual at a time,
-
it applies if there are bounds on statistical information, not just in the case where the statistical information is approximately precise, and
-
the statistical information does not actually have to be in the knowledge base; it just needs to be a logical consequence of it for sufficiently small tolerance vectors.
To make this precise, let X ={x1, …, xk} and C ={c1, …, ck} be sets of distinct variables and distinct constants, respectively. I write φ(X) to indicate that all of the free variables in the formula φ are in X; φ(C) denotes the new formula obtained by replacing each occurrences of xi in φ by ci. (Note that φ may contain other constants not among the cis; these are unaffected by the substitution.) Prove the following generalization of Theorem 11.3.2:
-
Let KB be a knowledge base of the form ψ(c) ∧ KB′ and assume that, for all sufficiently small tolerance vectors
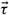 ,
,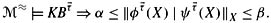
-
If no constant in C appears in KB′, in φ(X), orin ψ(X), then μ∞(φ(c) | KB) ∈ [α, β], provided the degree of belief exists.
(Note that the degree of belief may not exist since
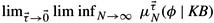 may not be equal to
may not be equal to 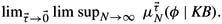 . However, it follows from the proof of the theorem that both of these limits lie in the interval [α, β]. This is why the limit does exist if α = β, as in Theorem 11.3.2.)
. However, it follows from the proof of the theorem that both of these limits lie in the interval [α, β]. This is why the limit does exist if α = β, as in Theorem 11.3.2.) -
-
*11.7 Prove Theorem 11.3.7. (Hint: For each domain size N and tolerance vector
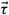 , partition
, partition 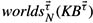 into clusters, where each cluster W′ is a maximal set satisfying the following four conditions:
into clusters, where each cluster W′ is a maximal set satisfying the following four conditions:-
All worlds in W′ agree on the denotation of every symbol in the vocabulary except possibly those appearing in φ(x) (so that, in particular, they agree on the denotation of the constant c).
-
All worlds in W′ also agree as to which elements satisfy ψ0(x); let this set be A0.
-
The denotation of symbols in φ must also be constant, except possibly when a member of A0 is involved. More precisely, let A0 be the set of domain elements {1, …, N}− A0. Then for any predicate symbol R or function symbol f of arity r appearing in φ(x), and for all worlds w, w′ ∈ W′, if d1, …, dr, dr+1 ∈ A0 then R(d1, …, dr) holds in w iff it holds in w′, and f(d1, …, dr) = dr +1 in w iff f(d1, …, dr) = dr +1 in w′. In particular, this means that for any constant symbol c′ appearing in φ(x), if it denotes d′ ∈ A0 in w, then it must denote d′ in w′.
-
All worlds in the cluster are isomorphic with respect to the vocabulary symbols in φ. (That is, if w and w′ are two worlds in the cluster, then there is a bijection on {1, …, n} such that for each symbol P in φ in the vocabulary, Pπ(w) is isomorphic to Pπ(w′) under f. For example, if P is a constant symbol d, then f(dπ(w)) = dπ(w′); similarly, if P is a binary predicate, the (d, d′) ∈ Pπ(w) iff (f (d), f(d′)) ∈ Pπ(w′).)
Then show that, within each cluster W′, the probability of φ(c) is within τi of α.)
-
-
11.8 First-order logic can express not only that there exists an individual that satisfies the formula φ(x), but that there exists a unique individual that satisfies φ(x). Let ∃!xφ(x) be an abbreviation for
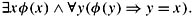
-
Show that (풜, 풱) ⊨ ∃!xφ(x) iff there is a unique d ∈ dom(풜) such that (풜, 풱[x/d]) ⊨ φ(x).
-
Generalize this to find a formula ∃N φ(x) that expresses the fact that exactly N individuals in the domain satisfy φ.
-
-
*11.9 Prove Theorem 11.3.8. (Hint: Suppose that α1, α2 > 0. Consider
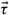 such that αi − τi > 0. Let βi = min(αi + τi, 1). For each domain size N, partition
such that αi − τi > 0. Let βi = min(αi + τi, 1). For each domain size N, partition 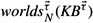 into clusters where each cluster W′ is a maximal set satisfying the following three conditions:
into clusters where each cluster W′ is a maximal set satisfying the following three conditions:-
All worlds in W′ agree on the denotation of every symbol in the vocabulary except for P. In particular, they agree on the denotations of c, ψ1, and ψ2. Let Ai be the denotation of ψi in W′ (i.e., Ai ={d ∈ D : w ⊨ ψ(d)} for w ∈ W′) and let ni = |Ai|).
-
All worlds in W′ have the same denotation of P for elements in A = {1, …, N}− (A1 ∪ A2).
-
For i = 1, 2, there exists a number ri such that all worlds in W′ have ri elements in Ai satisfying P.
Note that, since all worlds in W′ satisfy
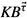 it follows that βi = ri/ni ∈ [αi − τi, αi + τi] for i = 1, 2. Show that the number of worlds in W′ satisfying P(c) is
it follows that βi = ri/ni ∈ [αi − τi, αi + τi] for i = 1, 2. Show that the number of worlds in W′ satisfying P(c) is 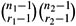 and the number of worlds satisfying P(c) is
and the number of worlds satisfying P(c) is 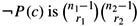 . Conclude from this that the fraction of worlds satisfying P(c) is
. Conclude from this that the fraction of worlds satisfying P(c) is 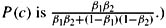
-
-
*11.10 State and prove a generalized version of Theorem 11.3.8 that allows more than two pieces of statistical information.
-
11.11 Complete the proof of Theorem 11.4.3.
-
*11.12 This exercise considers to what extent Rational Monotonicity holds in the random-worlds approach. Recall that Rational Monotonicity is characterized by axiom C5 in AXcond (see Section 8.6). Roughly speaking, it holds if the underlying likelihood measure is totally ordered. Since probability is totally ordered, it would seem that something like Rational Monotonicity should hold for the random-worlds approach, and indeed it does. Rational Monotonicity in the random-worlds framework is expressed as follows:
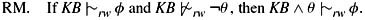
Show that the random-worlds approach satisfies the following weakened form of RM: If
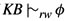 and
and 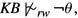 then
then 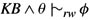 provided that μ∞(φ | KB ∧ θ) exists. Moreover, a sufficient condition for μ∞(φ | KB ∧ θ) to exist is that μ∞(θ | KB) exists.
provided that μ∞(φ | KB ∧ θ) exists. Moreover, a sufficient condition for μ∞(φ | KB ∧ θ) to exist is that μ∞(θ | KB) exists. -
11.13 The CUT property was introduced in Exercise 8.42 and shown to follow from P. In the setting of this chapter, CUT becomes
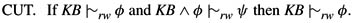
Show directly that CUT holds in the random-worlds approach. In fact, show that the following stronger result holds: If μ∞(φ | KB) = 1, then μ∞(ψ | KB) = μ∞(ψ | KB ∧ φ) (where equality here means that either neither limit exists or both do and are equal).
-
*11.14 This exercise shows that the random-worlds approach deals well with the lottery paradox.
-
Show that
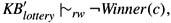 where KB′lottery is defined in Example 11.4.6. (Hint: Fix a domain size N. Cluster the worlds according to the number of ticket holders. That is, let Wk consist of all worlds with exactly k ticket holders. Observe that
where KB′lottery is defined in Example 11.4.6. (Hint: Fix a domain size N. Cluster the worlds according to the number of ticket holders. That is, let Wk consist of all worlds with exactly k ticket holders. Observe that 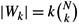 (since the winner must be one of the k ticket holders). Show that the fraction of worlds in Wk in which c wins is 1/k. Next, observe that
(since the winner must be one of the k ticket holders). Show that the fraction of worlds in Wk in which c wins is 1/k. Next, observe that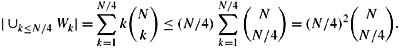
Similarly
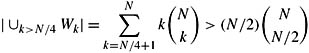
(since
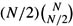 is just one term in the sum). Show that
is just one term in the sum). Show that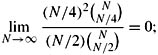
that is, for N sufficiently large, in almost all worlds there are at least N/4 ticket holders. The desired result now follows easily.)
-
Show that μ∞(Winner(c) | KB″lottery) = 1/N. (This actually follows easily from the first part of the analysis of part (a).)
-
-
11.15 Show that the random-worlds approach takes different constants to denote different individuals, by default. That is, show that if c and d are distinct constants, then
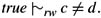 . The assumption that different individuals are distinct has been called the unique names assumption in the literature. This shows that the unique names assumption holds by default in the random-worlds approach.
. The assumption that different individuals are distinct has been called the unique names assumption in the literature. This shows that the unique names assumption holds by default in the random-worlds approach. -
*11.16 Consider a vocabulary 풯 consisting of k unary predicates P1, …, Pk and ℓ constant symbols. Let
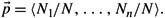 .
.-
Show that there are
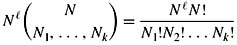
DN-풯-structures 풜 such that such that there are Ni domain elements satisfying Pi (i.e., |P풜i| = Ni).
-
Stirling's approximation says that
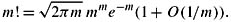
Using Stirling's approximation, show that there exist constants L and U such that
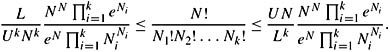
-
Let
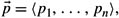 , where pi = Ni/N. Show that
, where pi = Ni/N. Show that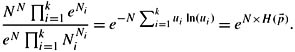
-
Conclude that
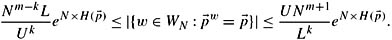
-
-
11.17 Show that μ∞(White(c) | true) = .5 and that
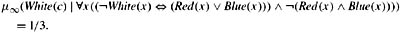
-
11.18 This exercise shows that random words does not support sampling, at least not in the most natural way.
-
Show that μ∞(Flies(Tweety) | Bird(Tweety)) = .5.
-
Show that μ∞(Flies(Tweety) | Bird(Tweety) ∧ KB′) = .5 if KB′ has the form
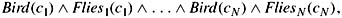
where Fliesi is either Flies or Flies for i = 1, …, N.
-
Show that if
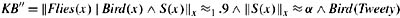
then μ∞(Flies(Tweety) | KB″) = .9α + .5(1 − α).
-
-
11.19 Suppose that 풯 = {P1, …, Pm, c1, …, cn}. That is, the vocabulary consists only of unary predicates and constants. Fix a domain size N. For each tuple (k1, …, km) such that 0 ≤ ki ≤ N, let W(k1, …, km) consist of all structures 풜 ∈ WN such that |Pi풜| = ki, for i = 1, …, N. Note that there are mN + 1 sets of the form W(k1, …, km). Let μN be the probability measure on WN such that μN (W(k1, …, km) = 1/mN+1 and all the worlds in W(k1, …, km) are equally likely.
-
Let 풜 ∈ WN be such that |Pi풜| = 0 (i.e., no individual satisfies any of P1, …, PN in 풜). What is μN(풜)?
-
Assume that N is even and let 풜 ∈ WN be such that |Pi풜| = N/2 for i = 1, …, N. What is μN(풜)?
You should get different answers for (a) and (b). Intuitively, μN does not make all worlds in WN equally likely, but it does make each possible cardinality of P1, …, PN equally likely. For φ, KB ∈
 fo(풯), define μ′∞(φ | KB) to be the common limit of
fo(풯), define μ′∞(φ | KB) to be the common limit of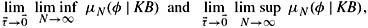
if the limit exists. μ′∞(φ | KB) gives a different way of obtaining degrees of belief from statistical information.
-
-
11.20 Show that the following simplified version of Theorem 11.3.2 holds for μ′∞:
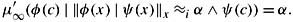
Actually, the general version of Theorem 11.3.2 also holds. Moreover, learning from samples works for μ′∞:
![]()
although the proof of this (which requires maximum entropy techniques) is beyond the scope of the book.
|
EAN: 2147483647
Pages: 140