11.4 Random Worlds and Default Reasoning

One of the most attractive features of the random-worlds approach is that it provides a well-motivated system of default reasoning, with a number of desirable properties. Recall that at the end of Chapter 10 I observed that if "birds typically fly" is interpreted as a statistical assertion and "Tweety flies" is interpreted as a statement about a (high) degree of belief, then in order to do default reasoning and, in particular, conclude that Tweety the bird flies from the fact that birds typically fly, there must be some way to connect statistical assertions with statements about degrees of belief. The randomworlds approach provides precisely such a connection.

The first step in exploiting this connection is to find an appropriate representation for "birds typically fly." The intuition here goes back to that presented in Chapter 8: "birds typically fly" should mean that birds are very likely to fly. Probabilistically, this should mean that the probability that a given bird flies is very high. As shown in Section 8.4.1, there are problems deciding how high is high enough: it will not work (in the sense of not giving System P) to take "high" to be "with probability greater than 1 − ∊" for some fixed ∊ . One way to deal with that problem, presented in Section 8.4.1, involves using sequences of probabilities. The language ^ is expressive enough to provide another approach—using approximate equality. "Birds typically fly" becomes ∥Flies(x)| Bird(x)∥_x ≈_i 1. (The exact choice of subscript on ≈ is not important, although if there are several defaults, it may be important to use different subscripts for each one; I return to this issue later.)

This way of expressing defaults can be used to express far more complicated defaults than can be represented in propositional logic, as the following examples show:

Example 11.4.1

Consider the fact that people who have at least one tall parent are typically tall. This default can be expressed in as

Example 11.4.2

Typicality statements can have nesting. For example, consider the nested default "typically, people who normally go to bed late normally rise late." This can be expressed using nested statistical assertions. The individuals who normally rise late are those who rise late most days; these are the individuals x satisfying ∥Rises-late(x, y) | Day(y)∥_y ≈₁ 1. Similarly, the individuals who normally go to bed late are those satisfying ∥To-bed-late(x, y′) | Day(y′)∥_y′ ≈₂ 1. Thus, the default can be captured by saying most individuals x that go to bed late also rise late:

On the other hand, the related default that "Typically, people who go to bed late rise late (the next morning)" can be expressed as

Representing typicality statements is only half the battle. What about a conclusion such as "Tweety flies"? This corresponds to a degree of belief of 1. More precisely, given a knowledge base KB (which, for example, may include ∥Flies(x) | Bird(x)∥_x ≈_i 1), the default conclusion "Tweety flies" follows from KB if μ_∞(Flies(Tweety) | KB) = 1.

The formula φ is a default conclusion from KB, written KB |∼_rw φ, if μ_∞(φ | KB) = 1. Note that it follows immediately from Theorem 11.3.2 that

That is, the conclusion "Tweety flies" does indeed follow from "Birds typically fly" and "Tweety is a bird." Moreover, if Tweety is a penguin then it follows that Tweety does not fly. That is, if

then it is immediate from Theorem 11.3.2 that

(The same conclusion would also hold if ∀x(Penguin(x) ⇒ Bird(x)) were replaced by Penguin(x) | Bird(x) _x ≈₃ 0; the latter formula is closer to what was used in Section 8.5, but the former better represents the actual state of affairs.)

In fact, the theorems of Section 11.3 show that quite a few other desirable conclusions follow. Before getting into them, I first establish that the relation |∼_rw satisfies the axioms of P described in Section 8.3, since these are considered the core properties of default reasoning.

Theorem 11.4.3

The relation |∼_rw satisfies the axioms of P. More precisely, the following properties hold if KB and KB′ are eventually consistent:

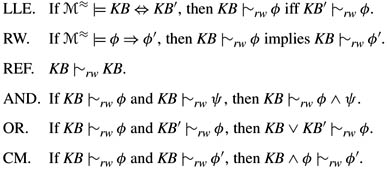
Proof LLE follows immediately from (indeed, is just a restatement of) Proposition 11.3.1. RW is immediate from the observation that if ≈ ⊨ φ ⇒ φ′ (provided that . REF is immediate from the fact that , provided that . I leave the proof of AND, OR, and CM to the reader (Exercise 11.11).

Not only does |∼_rw satisfy the axioms of P, it can go well beyond P. Let KB₁ be the knowledge base described earlier, which says that birds typically fly, penguins typically do not fly, penguins are birds, and Tweety is a penguin. Then the following are all immediate consequences of Theorems 11.3.2 and 11.3.7:

red penguins do not fly:
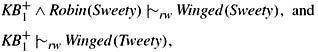
if birds typically have wings, then both robins and penguins have wings:

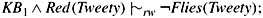
where KB⁺₁ is KB₁ ∧ ∥Winged(x) | Bird(x)∥_x ≈₃ 1 ∧∀x(Robin(x) ⇒ Bird(x));
if yellow things are typically easy to see, then yellow penguins are easy to see:

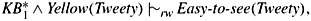
where KB*₁ is KB₁ ∧ ∥Easy-to-see(x) | Yellow(x)∥_x ≈₄ 1.

Thus, the random-worlds approach gives all the results that were viewed as desirable in Section 8.5 but could not be obtained by a number of extensions of P.

The next two examples show how the axioms of system P can be combined with Theorems 11.3.2 and 11.3.7 to give further results.

Example 11.4.4

Suppose that the predicates LU, LB, RU, and RB indicate, respectively, that the left arm is usable, the left arm is broken, the right arm is usable, and the right arm is broken. Let KB′_arm consist of the statements

∥LU(x)∥_x ≈₁ 1, ∥LU(x) | LB(x)∥_x ≈₂ 0 (left arms are typically usable, but not if they are broken),
∥RU(x)∥_x ≈₃ 1, ∥RU(x) | RB(x)∥_x ≈₄ 0 (right arms are typically usable, but not if they are broken).

Now, consider

the last conjunct of KB_arm just says that at least one of Eric's arms is broken (but does not specify which one or ones). From Theorem 11.3.2 it follows that

From Theorem 11.3.7, it follows that

The AND rule gives

and RW then gives

Similar reasoning shows that

The OR rule then gives

That is, by default it follows from KB_arm that exactly one of Eric's arms is usable, but no conclusions can be drawn as to which one it is. This seems reasonable: given that arms are typically not broken, knowing that at least one arm is broken should lead to the conclusion that exactly one is broken, but not which one it is.

Example 11.4.5

Recall that Example 11.4.2 showed how the nested typicality statement "typically, people who normally go to bed late normally rise late" can be expressed by the knowledge base KB_late:

Let KB′_late be

Taking ψ(x) to be ∥To-bed-late(x, y′) | Day(y′)∥_y′ ≈₂ 1and applying Theorem 11.3.2, it follows that Alice typically rises late. That is,

By Theorem 11.3.2 again, it follows that

The CUT Rule (Exercise 11.13) says that if KB |∼_rw φ and KB ∧ φ |∼_rw ψ, then KB |∼_rw ψ. Thus, KB′_late |∼_rw Rises-late(Alice, Tomorrow): by default, Alice will rise late tomorrow (and every other day, for that matter).

Finally, consider the lottery paradox from Examples 8.1.2 and 10.4.3.

Example 11.4.6

The knowledge base corresponding to the lottery paradox is just

This knowledge base is clearly eventually consistent. Moreover, it immediately follows from Theorem 11.3.2 that KB_lottery |∼_rw Winner(c) for any particular individual c. From RW, it is also immediate that KB_lottery |∼_rw ∃xWinner(x). The expected answer drops right out.

An objection to the use of the random-worlds approach here might be that it depends on the domain size growing unboundedly large. To simplify the analysis, suppose that exactly one person wins the lottery and that in order to win one must purchase a lottery ticket. Let Ticket(x) denote that x purchased a lottery ticket and let

With no further assumptions, it is not hard to show that KB′_lottery |∼_rw Winner(c), that is, μ_∞(Winner(c) | KB′_lottery) = 0 (Exercise 11.14(a)).

Now let KB″_lottery = KB′_lottery ∧∃^N x Ticket(x), where ∃^N x Ticket(x) is the formula stating that there are precisely N ticket holders. (This assertion can easily be expressed in first-order logic—see Exercise 11.8.) Then it is easy to see that μ_∞(Winner(c) | KB″_lottery) = 1/N. That is, the degree of belief that any particular individual c wins the lottery is 1/N. This numeric answer seems just right: it simply says that the lottery is fair. Note that this conclusion is not part of the knowledge base. Essentially, the random-worlds approach is concluding fairness in the absence of any other information.