2.5 THE NFA WITH -MOVES TO THE DFA

2.4 THE NFA WITH ˆˆ -MOVES

If a finite automata is modified to permit transitions without input symbols, along with zero, one, or more transitions on the input symbols, then we get an NFA with ˜ ˆˆ -moves, because the transitions made without symbols are called " ˆˆ -transitions."

Consider the NFA shown in Figure 2.4.

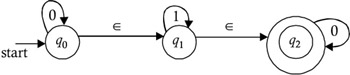
Figure 2.4: Finite automata with ˆˆ -moves.

This is an NFA with ˆˆ -moves because it is possible to transition from state q to q ₁ without consuming any of the input symbols. Similarly, we can also transition from state q ₁ to q ₂ without consuming any input symbols. Since it is a finite automata, an NFA with ˆˆ -moves will also be denoted as a five-tuple:

where Q , & pound ; , q , and F have the usual meanings, and defines a mapping from

(to take care of the ˆˆ -transitions as well as the non ˆˆ -transitions).

Acceptance of a String by the NFA with ˆˆ -Moves

A string x in * will ˆˆ -moves will be accepted by the NFA, if at least one path exists that corresponds to x starts in an initial state and ends in one of the final states. But since this path may be formed by ˆˆ -transitions as well as non- ˆˆ -transitions, to find out whether x is accepted or not by the NFA with ˆˆ -moves, we must define a function, ˆˆ -closure( q ), where q is a state of the automata.

The function ˆˆ -closure(q) is defined follows :

• ˆˆ -closure( q )= set of all those states of the automata that can be reached from q on a path labeled by ˆˆ .

• For example, in the NFA with ˆˆ -moves given above:

• ˆˆ -closure( q ) = { q , q ₁ , q ₂ }

• ˆˆ -closure( q ₁ ) = { q ₁ , q ₂ }

• ˆˆ -closure( q ₂ ) = { q ₂ }

The function

ˆˆ -closure ( q ) will never be an empty set, because q is always reachable from itself, without dependence on any input symbol; that is, on a path labeled by ˆˆ , q will always exist in ˆˆ -closure( q ) on that labeled path.

If P is a set of states, then the ˆˆ -closure function can be extended to find ˆˆ -closure( P ), as follows:

2.4.1 Algorithm for Finding ˆˆ -Closure(q)

Let T be the set that will comprise ˆˆ -closure( q ). We begin by adding q to T , and then initialize the stack by pushing q onto stack:

 while (stack not empty) do {  p  = pop (stack)  R  =   (  p  ,   )    for every member of  R  do      if it is not present in  T  then         {           add that member to  T  push member of  R  on stack         } } 

Since x is a member of *, and there may exist zero, one, or more transitions from a state on an input symbol, we define a new transition function, ₁ , which defines a mapping from 2 ^Q — * to 2 ^Q . If x is written as wa , where a is the last symbol of x and w is a string made of remaining symbols of x then:

since ₁ defines a mapping from 2 ^Q — * to 2 ^Q .

such that P contains at least one member of F and:

For example, in the NFA with ˆˆ -moves, given above, if x = 01, then to find out whether x is accepted by the automata or not, we proceed as follows:

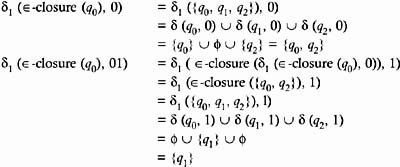
Therefore:

ˆˆ -closure( ₁ ( ˆˆ -closure (q ), 01) = ˆˆ -closure({q ₁ }) = {q ₁ , q ₂ } Since q ₂ is a final state, x = 01 is accepted by the automata.

Equivalence of NFA with ˆˆ -Moves to NFA Without ˆˆ -Moves

For every NFA with ˆˆ -moves, there exists an equivalent NFA without ˆˆ -moves that accepts the same language. To obtain an equivalent NFA without ˆˆ -moves, given an NFA with ˆˆ -moves, what is required is an elimination of ˆˆ -transitions from a given automata. But simply eliminating the ˆˆ -transitions from a given NFA with ˆˆ -moves will change the language accepted by the automata. Hence, for every ˆˆ -transition to be eliminated, we have to add some non- ˆˆ -transitions as substitutes in order to maintain the language's acceptance by the automata. Therefore, transforming an NFA with ˆˆ -moves to and NFA without ˆˆ -moves involves finding the non- ˆˆ -transitions that must be added to the automata for every ˆˆ -transition to be eliminated.

Consider the NFA with ˆˆ -moves shown in Figure 2.5.

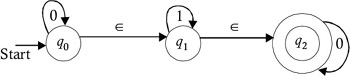
Figure 2.5: Transitioning from an ˆˆ -move NFA to a non- ˆˆ -move NFA.

There are ˆˆ -transitions from state q to q ₁ and from state q ₁ to q ₂ . To eliminate these ˆˆ -transitions, we must add a transition on 0 from q to q ₁ , as well as from state q to q ₂ . Similarly, a transition must be added on 1 from q to q ₁ , as well as from state q to q ₂ , because the presence of these ˆˆ -transitions in a given automata makes it possible to reach from q to q ₁ on consuming only 0, and it is possible to reach from q to q ₂ on consuming only 0. Similarly, it is possible to reach from q to q ₁ on consuming only 1, and it is possible to reach from q to q ₂ on consuming only 1. It is also possible to reach from q ₁ to q ₂ on consuming 0 as well as 1; and therefore, a transition from q ₁ to q ₂ on 0 and 1 is also required to be added. Since ˆˆ is also accepted by the given NFA ˆˆ -moves, to accept ˆˆ , and initial state of the NFA without ˆˆ -moves is required to be marked as one of the final states. Therefore, by adding these non- ˆˆ -transitions, and by making the initial state one of the final states, we get the automata shown in Figure 2.6.

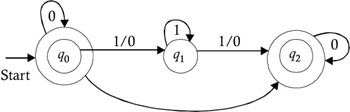
Figure 2.6: Making the initial state of the NFA one of the final states.

Therefore, when transforming an NFA with ˆˆ -moves into an NFA without ˆˆ -moves, only the transitions are required to be changed; the states are not required to be changed. But if a given NFA with q and ˆˆ -moves accepts ˆˆ (i.e., if the ˆˆ -closure ( q ) contains a member of F), then q is also required to be marked as one of the final states if it is not already a member of F. Hence:

If M = ( Q , , , q , F ) is an NFA with ˆˆ -moves, then its equivalent NFA without ˆˆ -moves will be M ₁ = ( Q , , ₁ , q , F ₁ )

where ₁ ( q , a ) = ˆˆ -closure( ( ˆˆ -closure( q ), a ))

and

• F ₁ = F ˆ ( q ) if ˆˆ -closure ( q ) contains a member of F

• F ₁ = F otherwise

For example, consider the following NFA with ˆˆ -moves:

where

		1	ˆˆ
q	{ q }		{ q 1 }
q 1		{ q 1 }	{ q 2 }
q 2		{ q 2 }

Its equivalent NFA without ˆˆ -moves will be:

where

1		1
q	{ q , q 1 , q 2 }	{ q 1 , q 2 }
q 1		{ q 1 , q 2 }
q 2		{ q 2 }

Since there exists a DFA for every NFA without ˆˆ -moves, and for every NFA with ˆˆ -moves there exists an equivalent NFA without ˆˆ -moves, we conclude that for every NFA with ˆˆ -moves there exists a DFA.