Algorithms

Objective:

Understand symmetric encryption

Understand asymmetric encryption

As introduced previously, an algorithm is a set of rules used to encrypt and decrypt data. It's the set of instructions used along with the cryptographic key to encrypt plaintext data. Plaintext data encrypted with different keys or dissimilar algorithms will produce different ciphertext. Not all cryptosystems are of the same strength. For example, Caesar might have thought his system of encryption was quite strong, but it would be relativity insecure today. How strong should an encryption process be? The strength of a cryptosystem will rely on the strength of an algorithm itself, as a flawed algorithm can be reversed, and the cryptographic key recovered. The encryption mechanism's strength also depends on the value of the data. High value data requires more protection than data that has little value. More valuable information needs longer key lengths and more frequent key exchange to protect against attacks. Another key factor is how long the data will be valid for. If the data is valid only for seconds, a lower encryption algorithm could be used.

Modern cryptographic systems use two types of algorithms for encrypting and decrypting data. Symmetric encryption uses the same key to encode and decode data. Asymmetric encryption uses different keys for encryption and decryption. Each participant is assigned a pair of keys. Before each type is examined in more detail, spend a minute to review Table 12.1, which highlights some of the key advantages and disadvantages of each method.

Table 12.1. Symmetric and Asymmetric Differences

Type of Encryption	Advantages	Disadvantages
Symmetric	Faster than asymmetric	Key distribution
		Only provides confidentiality
Asymmetric	Easy key exchange	Slower than symmetric
	Can provide confidentiality and authentication

Exam Alert

Make sure that you know the differences between symmetric and asymmetric encryption.

 

Symmetric Encryption

Symmetric encryption is the older of the two forms of encryption. It uses a single shared secret key for encryption and decryption. Symmetric algorithms include

• DES Data Encryption Standard is the most common symmetric algorithm used.
• Blowfish A general-purpose symmetric algorithm intended as a replacement for DES.
• Rijndael A block cipher adopted as the AES by the U.S. government to replace DES.
• RC4 Rivest Cipher 4 is a stream-based cipher.
• RC5 Rivest Cipher 5 is a block-based cipher.
• SAFER Secure and Fast Encryption Routine is a block-based cipher.

All symmetric algorithms are based on the single shared key concept. An example of this can be seen in Figure 12.2.

Figure 12.2. Symmetric encryption.

This simple diagram shows the process that symmetric encryption entails. Plaintext is encrypted with the single shared key and is then transmitted to the message recipient who goes through the same process to decrypt the message. The dual use of keys is what makes this system so simple, and it also causes its weakness. Symmetric encryption is fast and can encrypt and decrypt quickly; it also is considered strong. Symmetric encryption is hard to break if a large key is used. Even though symmetric encryption has it strengths, it also has three disadvantages.

The first problem with symmetric encryption is key distribution. For symmetric encryption to be effective, there must be a secure method in which to transfer keys. In the modern world, there needs to be some type of out-of-band transmission. For example, if Bob wants to send Alice a secret message but is afraid that Black Hat Bill can monitor their communication, how can he send the message? If the key is sent in cleartext, Black Hat Bill can intercept it. Bob could deliver the key in person, mail it, or even send a courier. All these methods are highly impractical in the world of ecommerce and electronic communication.

Even if the problems of key exchange are overcome, you still are faced with a second problem, key management. If, for example, you needed to communicate with 10 people using symmetric encryption, you would need 45 keys. The following formula is used to calculate the number of keys needed: N(N1)/2 or [10(101)/2 = 45 keys]. Key management becomes the second big issue when dealing with symmetric encryption.

The third and final problem of symmetric encryption is that it provides confidentiality. If you're looking for authentication, you will have to consider asymmetric encryption. But before asymmetric encryption is discussed, let's take a look at DES, one of the most popular forms of symmetric encryption.

Data Encryption Standard (DES)

DES was developed more than 20 years ago by the National Bureau of Standards (NBS). NBS is now known as the National Institute of Standards and Technology (NIST). DES wasn't developed in a vacuum; it was actually a joint project between NBS and IBM. IBM had already developed an algorithm called Lucifer. This algorithm was modified to use a 56-bit key and was finally adopted as a national standard in 1976. The certification as a national standard is not a permanent thing; therefore, DES was required to be recertified every five years. While initially passing without any problems, DES begin to encounter problems during the 1987 recertification. By 1993, NIST stated that DES was beginning to outlive its usefulness, and NIST began looking for candidates to replace it. This new standard was to be referred to as the Advanced Encryption Standard (AES). What happened to DES? Well, DES had become the victim of increased computing power. Just as Moore's law had predicted, processing power has doubled about every 18 to 24 months. The result is that each year it becomes easier to brute force existing encryption standards. A good example can be seen in the big encryption news of 1998 when it was announced that The Electronic Frontier Foundation (EFF) was able to crack DES in about 23 hours. The attack used distributed computing and required over 100,000 computers. That's more processing power than most of us have at home, but it demonstrates the need for stronger algorithms.

DES functions by what is known as a block cipher. The other type of cipher is a stream cipher. Block and stream ciphers can be defined as follows:

• Block Ciphers Functions by dividing the message into blocks for processing.
• Stream Ciphers Functions by dividing the message into bits for processing.

Because DES is a block cipher, it segments the input data into blocks. DES processes 64 bits of plaintext at a time to output 64-bit blocks of ciphertext. DES uses a 56-bit key, whereas the remaining eight bits are used for parity. Because it is symmetric encryption, a block cipher uses the same key to encrypt and decrypt. DES actually works by means of a substitution cipher. It then performs a permutation on the input. This action is called a round, and DES performs this 16 times on every 64-bit block. DES actually has four modes or types, and not all of these are of equal strength. The four modes of DES include: Electronic Codebook (ECB) mode, Cipher Block Chaining (CBC) mode, Cipher Feedback (CFB) mode, and Output Feedback (OFB) mode, which are all explained in the following list:

• Electronic Codebook mode (ECB) ECB is the native encryption mode of DES. It produces the highest throughput, although it is the easiest form of DES to break. The same plaintext encrypted with the same key always produces the same ciphertext.
• Cipher Block Chaining mode (CBC) The CBC mode of DES is widely used and is similar to ECB. CBC takes data from one block to be used in the next; therefore, it chains the blocks together. However, it's more secure than ECB and harder to crack. The disadvantage of CBC is that errors in one block will be propagated to others, which might make it impossible to decrypt that block and the following blocks as well.
• Cipher Feedback mode (CFB) CFB emulate a stream cipher. CFB can be used to encrypt individual characters. Like CBC, errors and corruption can propagate through the encryption process.
• Output Feedback mode (OFB) OFB also emulates a stream cipher. Unlike CFB, transmission errors do not propagate throughout the encryption process because OFB uses plaintext to feedback into a stream of ciphertext.

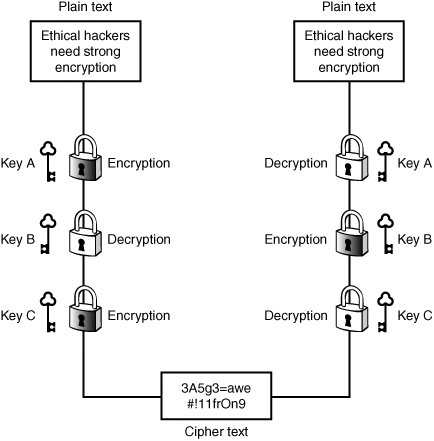
To extend the usefulness of the DES encryption standard, 3DES was implemented. 3DES can use two or three keys to encrypt data and performs what is referred to as multiple encryption. It has a key length of 168 bit. While it is much more secure, it is up to three times as slow as 56-bit DES. An example of three key 3DES is shown in Figure 12.3.

Figure 12.3. 3DES (Triple DES).

Exam Alert

Double DES is not used, as it is no more secure than regular DES and is vulnerable to a meet-in-the-middle attack.

 

Advanced Encryption Standard (AES)

In 2002, NIST decided on the replacement for DES. Rijndael (which sounds like rain doll) was the chosen replacement. Its name is derived from its two developers Vincent Rijmen and Joan Daemen. Rijndael is an iterated block cipher that supports variable key and block lengths of 128, 192, or 256 bits. It is considered a fast, simple, and robust encryption mechanism. Rijndael is also known to stand up well to various types of attacks. It uses a four-step, parallel series of rounds. Each of these steps is performed during each round. They include

• Byte sub Each byte is replaced by an S-box substation.
• Shift row Bytes are arranged in a rectangle and shifted.
• Mix column Matrix multiplication is performed based on the arranged rectangle.
• Add round key This round's subkey is cored in.

Rivest Cipher (RC)

Rivest cipher is a general term for the family of ciphers all designed by Ron Rivest. These include RC2, RC4, RC5, and RC6. RC2 is an early algorithm in the series. It features a variable key-size, 64-bit block cipher that can be used as a drop-in substitute for DES. RC4 is a stream cipher and is faster than block mode ciphers. The 40-bit version was originally available in Wired Equivalent Privacy (WEP). RC4 is most commonly found in 128-bit key version. RC5 is a block-based cipher in which the number of rounds can range from 0 to 255 and the key can range from 0 bits to 2040 bits in size. Finally, there is RC6. It features variable key size and rounds and added two features not found in RC5 integer multiplication and four 4-bit working registers.

Asymmetric Encryption (Public Key Encryption)

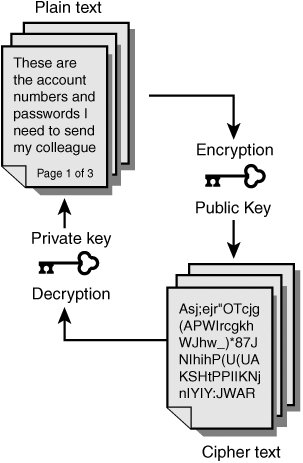
Asymmetric encryption is a rather new discovery Dr. W Diffie and Dr M.E Hellman developed the first public key exchange protocol in 1976. Public key cryptography is made possible by the use of one-way functions. It's different from symmetric encryption because it requires two keys. What one key does, the second key undoes. These keys are referred to as public and private keys. The public key can be published and given to anyone, although the user keeps the private key a secret. An example of public key encryption can be seen in Figure 12.4.

Figure 12.4. Asymmetric encryption.

Asymmetric encryption is different from symmetric encryption in other ways because it uses difficult mathematical problems. Specifically, it is called a trapdoor function. Trapdoor functions get their name from the difficulty in factoring large prime numbers. For example, given the prime numbers of 387 and 283, it is easy to multiply them together and get 109,521.

However, if you are given the number 109,521, it's quite difficult to extract the two prime numbers of 387 and 283. As you can see, anyone who knows the trapdoor can perform the function easily in both directions, but anyone lacking the trapdoor can perform the function only in one direction. Trapdoor functions can be used in the forward direction for encryption and signature verification, whereas the inverse direction is used for decryption and signature generation. Although factoring large prime numbers is specific to RSA, it is not the only type; there are others such as the Discrete Logarithm Problem. RSA, Diffie-Hellman, ECC, and El Gamal are all popular asymmetric algorithms. All these functions are examined next.

Exam Alert

It is essential to understand the following principle in public key encryption: What A encrypts, B decrypts; what B encrypts, A decrypts.

 

RSA

RSA was developed in 1977 at MIT by Ron Rivest, Adi Shamir, and Leonard Adleman, and it is one of the first public key encryption systems ever invented. Although RSA is not as fast a symmetric encryption, it is strong. It gets its strength by using two large prime numbers. It works on the principle of factoring these large prime numbers. RSA key sizes can grow quite large. RFC 2537 states, "For interoperability of RSA, the exponent and modulus are each currently limited to 4096 bits in length." Cracking a key of this size would require an extraordinary amount of computer processing power and time.

RSA is used for both encryption and digital signatures. Because asymmetric encryption is not as fast as symmetric encryption, many times the two are used together. Therefore, it gains the strengths of both systems. The asymmetric protocol is used to exchange the private key while the actual communication is performed with symmetric encryption. The RSA cryptosystem can be found in many products, such as Microsoft Internet Explorer and Mozilla Firefox.

Diffie-Hellman

Diffie-Hellman is another widely used asymmetric encryption protocol. It was developed for use as a key exchange protocol, and it is used in Secure Sockets Layer (SSL) and IPSec. Diffie-Hellman is extremely valuable because it allows two individuals to exchange keys that have not communicated with each other before. However, like most systems, it isn't perfect, as it can be vulnerable to man-in-the-middle attacks. This is because the key exchange process does not authenticate the participants by default. This vulnerability can be overcome if you use digital signatures.

El Gamal

Developed in the early 1980s, El Gamal was to be used for encryption and digital signatures. It is composed of three discrete components, including a key generator, an encryption algorithm, and a decryption algorithm. It's somewhat different from the other asymmetric systems that have been discussed because it is based not on the factoring of prime numbers, but rather on the difficulty of solving discrete logarithm problems.

Elliptic Curve Cryptosystem (ECC)

ECC uses the discrete logarithm problem over the points on an elliptic curve in the encryption and decryption processes to provide security to messages. Because it requires less processing power than some of the previous algorithms discussed, it's useful in hardware devices, such as cell phones and PDAs.

How Strong Is ECC?

In early 2000, the French National Institute in Computer Science and Control wanted to test ECC's strength. ECC is used in applications such as Wireless Application Protocol standards and in an optimized version of the Wireless Transport Layer Security protocol.

Using a distributed network of more than 9,500 computers, it was able to brute force ECC and recover the 109-bit key that had been used to encrypt a message. The key was found by trying every possible combination until one was found that worked. Now, if you're thinking that you might try and break ECC yourself on your home computer, it's calculated that on a single machine, it would take almost 500 years. If a larger key were used, it would take even longer. Therefore, although brute force attacks are possible, they are extremely time-consuming and computationally intensive.

Hashing